Geometric Algorithms for $k$-NN Poisoning

We propose a label poisoning attack on geometric data sets against $k$-nearest neighbor classification. We provide an algorithm that can compute an $\varepsilon n$-additive approximation of the optimal poisoning in $n\cdot 2^{2^{O(d+k/\varepsilon)}}$ time for a given data set $X \in \mathbb{R}^d$, where $|X| = n$. Our algorithm achieves its objectives through the application of multi-scale random partitions.

Learning Lines with Ordinal Constraints

We study the problem of finding a mapping $f$ from a set of points into the real line, under ordinal triple constraints. An ordinal constraint for a triple of points $(u,v,w)$ asserts that $|f(u)-f(v)|<|f(u)-f(w)|$. We present an approximation algorithm for the dense case of this problem. Given an instance that admits a solution that satisfies $(1-\varepsilon)$-fraction of all constraints, our algorithm computes a solution that satisfies $(1-O(\varepsilon^{1/8}))$-fraction of all constraints, in time $O(n^7) + (1/\varepsilon)^{O(1/\varepsilon^{1/8})} n$.

Learning Mahalanobis Metric Spaces via Geometric Approximation Algorithms

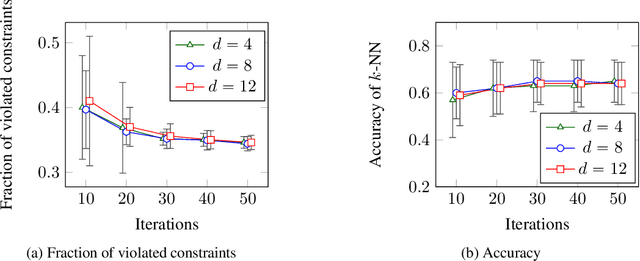
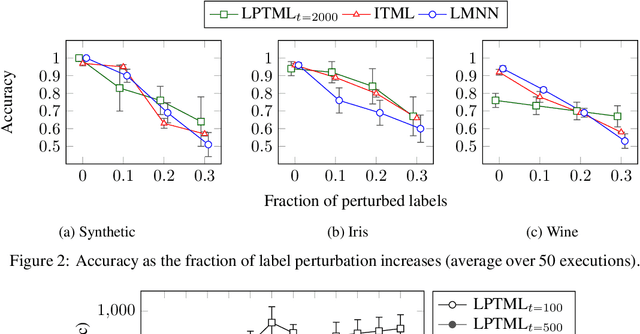
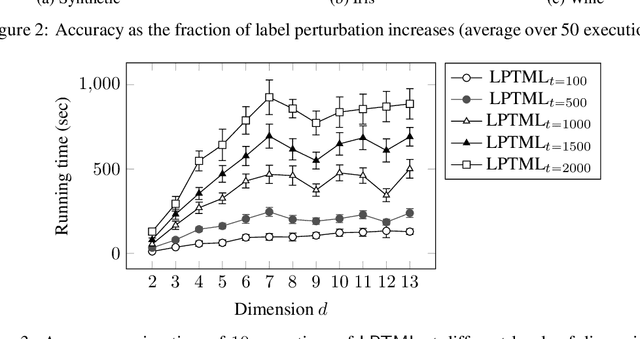
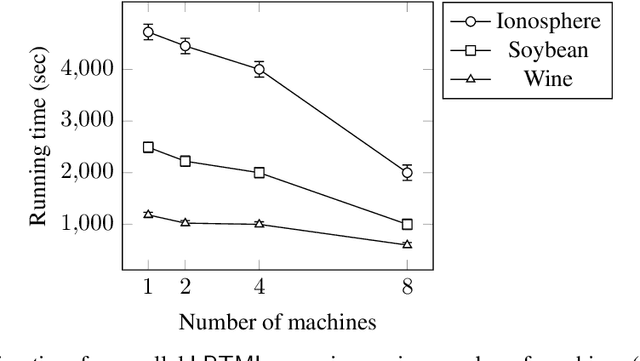
Learning Mahalanobis metric spaces is an important problem that has found numerous applications. Several algorithms have been designed for this problem, including Information Theoretic Metric Learning (ITML) by [Davis et al. 2007] and Large Margin Nearest Neighbor (LMNN) classification by [Weinberger and Saul 2009]. We consider a formulation of Mahalanobis metric learning as an optimization problem, where the objective is to minimize the number of violated similarity/dissimilarity constraints. We show that for any fixed ambient dimension, there exists a fully polynomial-time approximation scheme (FPTAS) with nearlylinear running time. This result is obtained using tools from the theory of linear programming in low dimensions. We also discuss improvements of the algorithm in practice, and present experimental results on synthetic and real-world data sets.

Algorithms for metric learning via contrastive embeddings

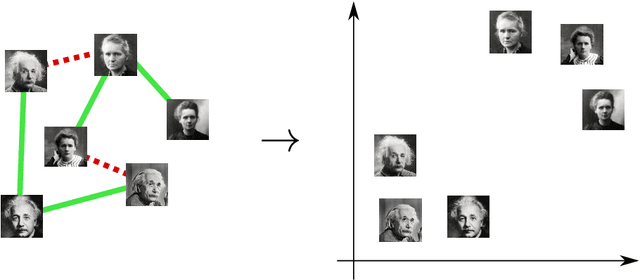
We study the problem of supervised learning a metric space under discriminative constraints. Given a universe $X$ and sets ${\cal S}, {\cal D}\subset {X \choose 2}$ of similar and dissimilar pairs, we seek to find a mapping $f:X\to Y$, into some target metric space $M=(Y,\rho)$, such that similar objects are mapped to points at distance at most $u$, and dissimilar objects are mapped to points at distance at least $\ell$. More generally, the goal is to find a mapping of maximum accuracy (that is, fraction of correctly classified pairs). We propose approximation algorithms for various versions of this problem, for the cases of Euclidean and tree metric spaces. For both of these target spaces, we obtain fully polynomial-time approximation schemes (FPTAS) for the case of perfect information. In the presence of imperfect information we present approximation algorithms that run in quasipolynomial time (QPTAS). Our algorithms use a combination of tools from metric embeddings and graph partitioning, that could be of independent interest.

Near-Optimal Sample Complexity Bounds for Maximum Likelihood Estimation of Multivariate Log-concave Densities

We study the problem of learning multivariate log-concave densities with respect to a global loss function. We obtain the first upper bound on the sample complexity of the maximum likelihood estimator (MLE) for a log-concave density on $\mathbb{R}^d$, for all $d \geq 4$. Prior to this work, no finite sample upper bound was known for this estimator in more than $3$ dimensions. In more detail, we prove that for any $d \geq 1$ and $\epsilon>0$, given $\tilde{O}_d((1/\epsilon)^{(d+3)/2})$ samples drawn from an unknown log-concave density $f_0$ on $\mathbb{R}^d$, the MLE outputs a hypothesis $h$ that with high probability is $\epsilon$-close to $f_0$, in squared Hellinger loss. A sample complexity lower bound of $\Omega_d((1/\epsilon)^{(d+1)/2})$ was previously known for any learning algorithm that achieves this guarantee. We thus establish that the sample complexity of the log-concave MLE is near-optimal, up to an $\tilde{O}(1/\epsilon)$ factor.