Algorithms for metric learning via contrastive embeddings
Paper and Code
Jul 13, 2018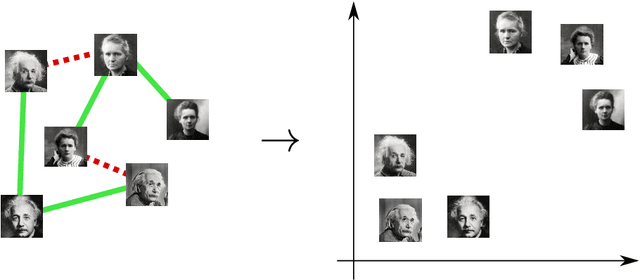
We study the problem of supervised learning a metric space under discriminative constraints. Given a universe $X$ and sets ${\cal S}, {\cal D}\subset {X \choose 2}$ of similar and dissimilar pairs, we seek to find a mapping $f:X\to Y$, into some target metric space $M=(Y,\rho)$, such that similar objects are mapped to points at distance at most $u$, and dissimilar objects are mapped to points at distance at least $\ell$. More generally, the goal is to find a mapping of maximum accuracy (that is, fraction of correctly classified pairs). We propose approximation algorithms for various versions of this problem, for the cases of Euclidean and tree metric spaces. For both of these target spaces, we obtain fully polynomial-time approximation schemes (FPTAS) for the case of perfect information. In the presence of imperfect information we present approximation algorithms that run in quasipolynomial time (QPTAS). Our algorithms use a combination of tools from metric embeddings and graph partitioning, that could be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge