Diego Ihara Centurion
Geometric Algorithms for $k$-NN Poisoning
Jun 21, 2023Abstract:We propose a label poisoning attack on geometric data sets against $k$-nearest neighbor classification. We provide an algorithm that can compute an $\varepsilon n$-additive approximation of the optimal poisoning in $n\cdot 2^{2^{O(d+k/\varepsilon)}}$ time for a given data set $X \in \mathbb{R}^d$, where $|X| = n$. Our algorithm achieves its objectives through the application of multi-scale random partitions.
Learning Lines with Ordinal Constraints
May 25, 2020Abstract:We study the problem of finding a mapping $f$ from a set of points into the real line, under ordinal triple constraints. An ordinal constraint for a triple of points $(u,v,w)$ asserts that $|f(u)-f(v)|<|f(u)-f(w)|$. We present an approximation algorithm for the dense case of this problem. Given an instance that admits a solution that satisfies $(1-\varepsilon)$-fraction of all constraints, our algorithm computes a solution that satisfies $(1-O(\varepsilon^{1/8}))$-fraction of all constraints, in time $O(n^7) + (1/\varepsilon)^{O(1/\varepsilon^{1/8})} n$.
Algorithms for metric learning via contrastive embeddings
Jul 13, 2018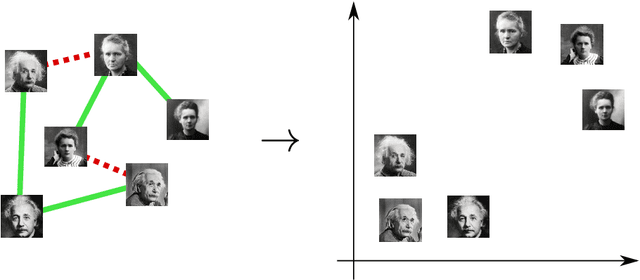
Abstract:We study the problem of supervised learning a metric space under discriminative constraints. Given a universe $X$ and sets ${\cal S}, {\cal D}\subset {X \choose 2}$ of similar and dissimilar pairs, we seek to find a mapping $f:X\to Y$, into some target metric space $M=(Y,\rho)$, such that similar objects are mapped to points at distance at most $u$, and dissimilar objects are mapped to points at distance at least $\ell$. More generally, the goal is to find a mapping of maximum accuracy (that is, fraction of correctly classified pairs). We propose approximation algorithms for various versions of this problem, for the cases of Euclidean and tree metric spaces. For both of these target spaces, we obtain fully polynomial-time approximation schemes (FPTAS) for the case of perfect information. In the presence of imperfect information we present approximation algorithms that run in quasipolynomial time (QPTAS). Our algorithms use a combination of tools from metric embeddings and graph partitioning, that could be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge