Learning Mahalanobis Metric Spaces via Geometric Approximation Algorithms
Paper and Code
May 24, 2019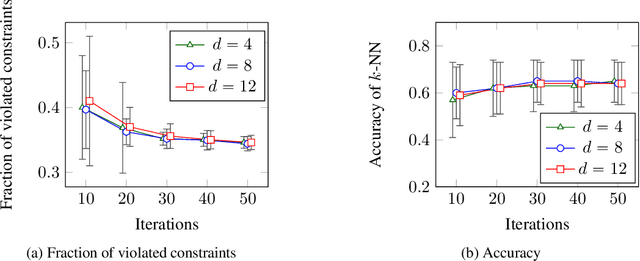
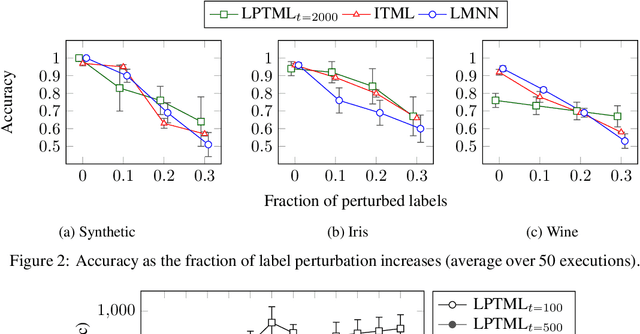
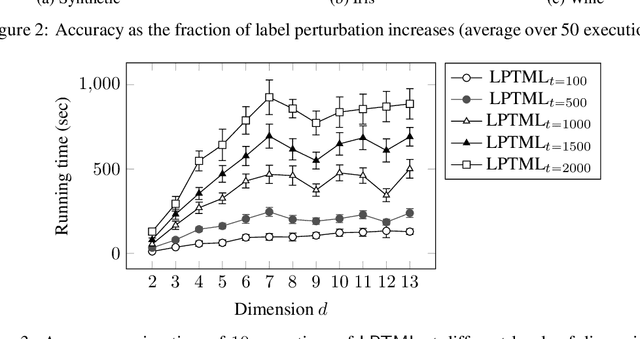
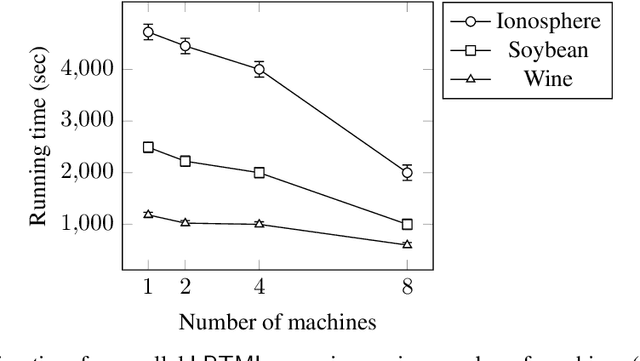
Learning Mahalanobis metric spaces is an important problem that has found numerous applications. Several algorithms have been designed for this problem, including Information Theoretic Metric Learning (ITML) by [Davis et al. 2007] and Large Margin Nearest Neighbor (LMNN) classification by [Weinberger and Saul 2009]. We consider a formulation of Mahalanobis metric learning as an optimization problem, where the objective is to minimize the number of violated similarity/dissimilarity constraints. We show that for any fixed ambient dimension, there exists a fully polynomial-time approximation scheme (FPTAS) with nearlylinear running time. This result is obtained using tools from the theory of linear programming in low dimensions. We also discuss improvements of the algorithm in practice, and present experimental results on synthetic and real-world data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge