Amine Ouasfi
Sparfels: Fast Reconstruction from Sparse Unposed Imagery
May 04, 2025Abstract:We present a method for Sparse view reconstruction with surface element splatting that runs within 3 minutes on a consumer grade GPU. While few methods address sparse radiance field learning from noisy or unposed sparse cameras, shape recovery remains relatively underexplored in this setting. Several radiance and shape learning test-time optimization methods address the sparse posed setting by learning data priors or using combinations of external monocular geometry priors. Differently, we propose an efficient and simple pipeline harnessing a single recent 3D foundation model. We leverage its various task heads, notably point maps and camera initializations to instantiate a bundle adjusting 2D Gaussian Splatting (2DGS) model, and image correspondences to guide camera optimization midst 2DGS training. Key to our contribution is a novel formulation of splatted color variance along rays, which can be computed efficiently. Reducing this moment in training leads to more accurate shape reconstructions. We demonstrate state-of-the-art performances in the sparse uncalibrated setting in reconstruction and novel view benchmarks based on established multi-view datasets.
ProKeR: A Kernel Perspective on Few-Shot Adaptation of Large Vision-Language Models
Jan 19, 2025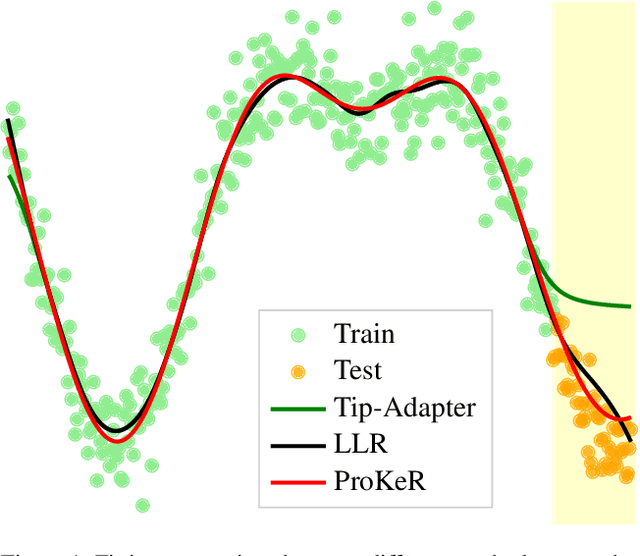
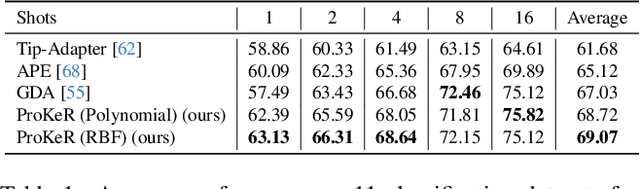
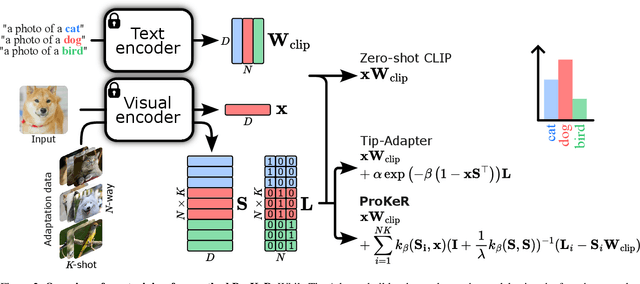
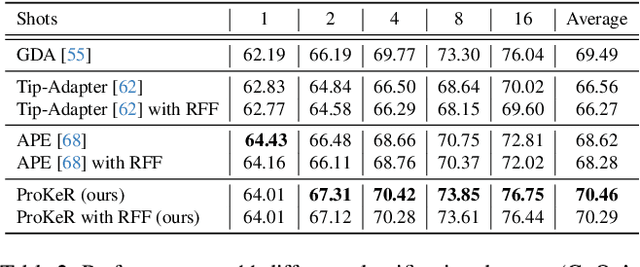
Abstract:The growing popularity of Contrastive Language-Image Pretraining (CLIP) has led to its widespread application in various visual downstream tasks. To enhance CLIP's effectiveness and versatility, efficient few-shot adaptation techniques have been widely adopted. Among these approaches, training-free methods, particularly caching methods exemplified by Tip-Adapter, have gained attention for their lightweight adaptation without the need for additional fine-tuning. In this paper, we revisit Tip-Adapter from a kernel perspective, showing that caching methods function as local adapters and are connected to a well-established kernel literature. Drawing on this insight, we offer a theoretical understanding of how these methods operate and suggest multiple avenues for enhancing the Tip-Adapter baseline. Notably, our analysis shows the importance of incorporating global information in local adapters. Therefore, we subsequently propose a global method that learns a proximal regularizer in a reproducing kernel Hilbert space (RKHS) using CLIP as a base learner. Our method, which we call ProKeR (Proximal Kernel ridge Regression), has a closed form solution and achieves state-of-the-art performances across 11 datasets in the standard few-shot adaptation benchmark.
Toward Robust Neural Reconstruction from Sparse Point Sets
Dec 20, 2024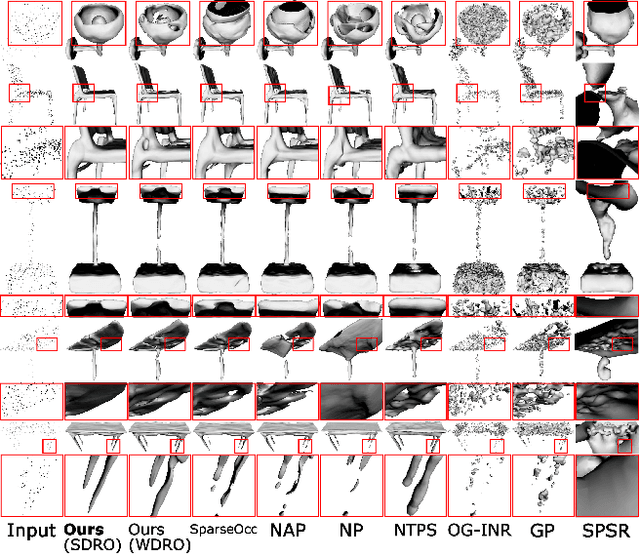
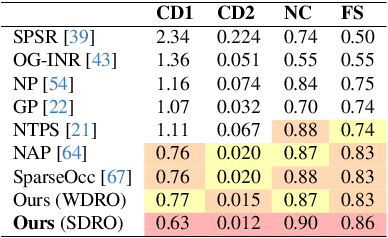
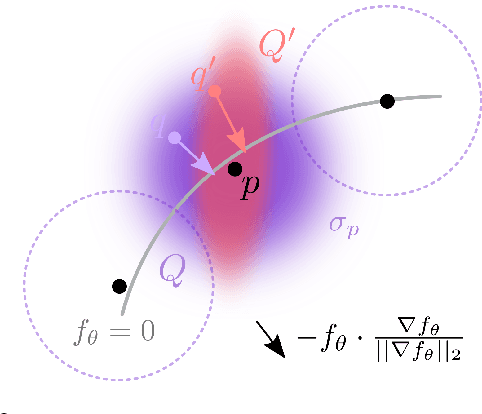
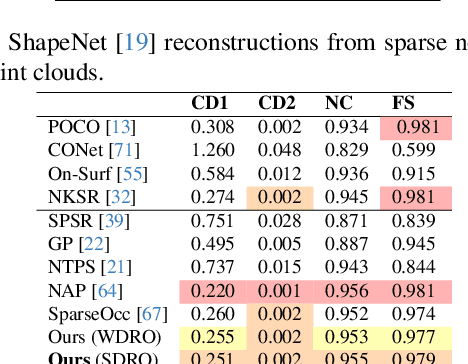
Abstract:We consider the challenging problem of learning Signed Distance Functions (SDF) from sparse and noisy 3D point clouds. In contrast to recent methods that depend on smoothness priors, our method, rooted in a distributionally robust optimization (DRO) framework, incorporates a regularization term that leverages samples from the uncertainty regions of the model to improve the learned SDFs. Thanks to tractable dual formulations, we show that this framework enables a stable and efficient optimization of SDFs in the absence of ground truth supervision. Using a variety of synthetic and real data evaluations from different modalities, we show that our DRO based learning framework can improve SDF learning with respect to baselines and the state-of-the-art methods.
Few-Shot Unsupervised Implicit Neural Shape Representation Learning with Spatial Adversaries
Aug 27, 2024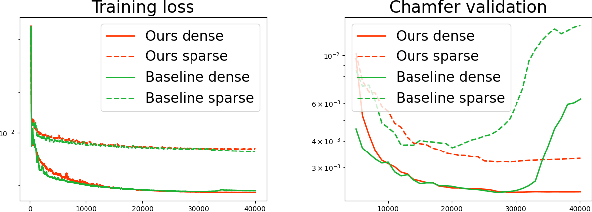

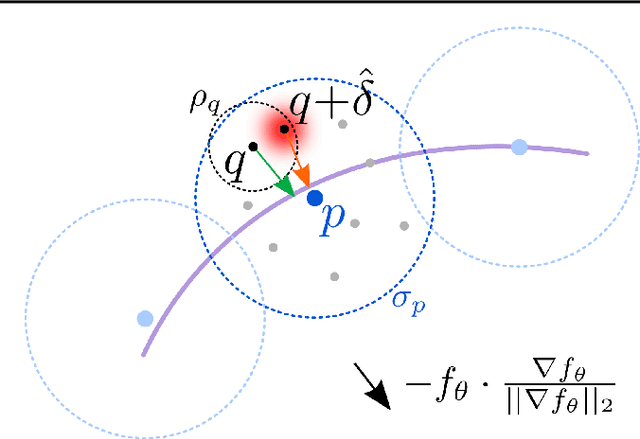
Abstract:Implicit Neural Representations have gained prominence as a powerful framework for capturing complex data modalities, encompassing a wide range from 3D shapes to images and audio. Within the realm of 3D shape representation, Neural Signed Distance Functions (SDF) have demonstrated remarkable potential in faithfully encoding intricate shape geometry. However, learning SDFs from sparse 3D point clouds in the absence of ground truth supervision remains a very challenging task. While recent methods rely on smoothness priors to regularize the learning, our method introduces a regularization term that leverages adversarial samples around the shape to improve the learned SDFs. Through extensive experiments and evaluations, we illustrate the efficacy of our proposed method, highlighting its capacity to improve SDF learning with respect to baselines and the state-of-the-art using synthetic and real data.
SparseCraft: Few-Shot Neural Reconstruction through Stereopsis Guided Geometric Linearization
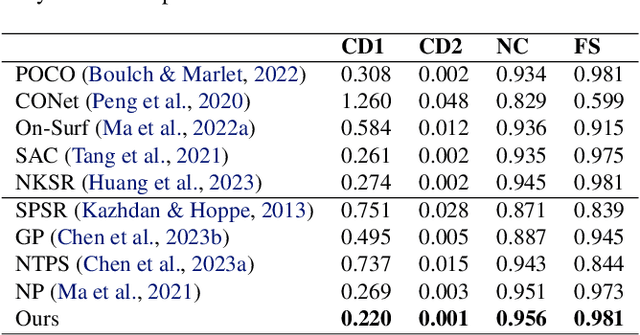
Jul 19, 2024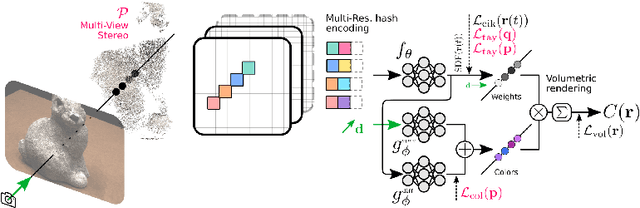
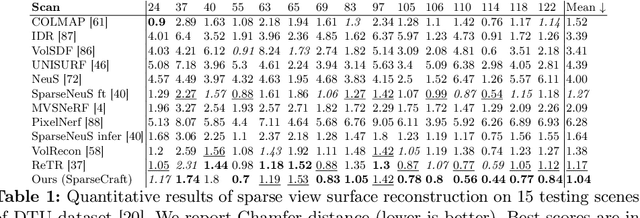

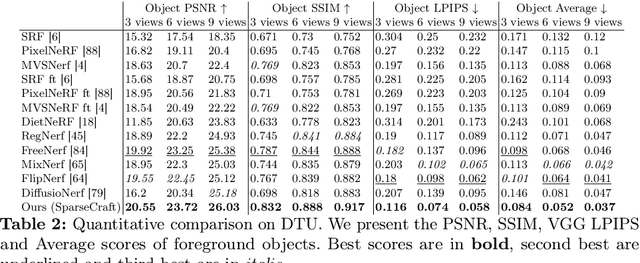
Abstract:We present a novel approach for recovering 3D shape and view dependent appearance from a few colored images, enabling efficient 3D reconstruction and novel view synthesis. Our method learns an implicit neural representation in the form of a Signed Distance Function (SDF) and a radiance field. The model is trained progressively through ray marching enabled volumetric rendering, and regularized with learning-free multi-view stereo (MVS) cues. Key to our contribution is a novel implicit neural shape function learning strategy that encourages our SDF field to be as linear as possible near the level-set, hence robustifying the training against noise emanating from the supervision and regularization signals. Without using any pretrained priors, our method, called SparseCraft, achieves state-of-the-art performances both in novel-view synthesis and reconstruction from sparse views in standard benchmarks, while requiring less than 10 minutes for training.
Unsupervised Occupancy Learning from Sparse Point Cloud
Apr 03, 2024Abstract:Implicit Neural Representations have gained prominence as a powerful framework for capturing complex data modalities, encompassing a wide range from 3D shapes to images and audio. Within the realm of 3D shape representation, Neural Signed Distance Functions (SDF) have demonstrated remarkable potential in faithfully encoding intricate shape geometry. However, learning SDFs from 3D point clouds in the absence of ground truth supervision remains a very challenging task. In this paper, we propose a method to infer occupancy fields instead of SDFs as they are easier to learn from sparse inputs. We leverage a margin-based uncertainty measure to differentially sample from the decision boundary of the occupancy function and supervise the sampled boundary points using the input point cloud. We further stabilize the optimization process at the early stages of the training by biasing the occupancy function towards minimal entropy fields while maximizing its entropy at the input point cloud. Through extensive experiments and evaluations, we illustrate the efficacy of our proposed method, highlighting its capacity to improve implicit shape inference with respect to baselines and the state-of-the-art using synthetic and real data.
Robustifying Generalizable Implicit Shape Networks with a Tunable Non-Parametric Model
Nov 21, 2023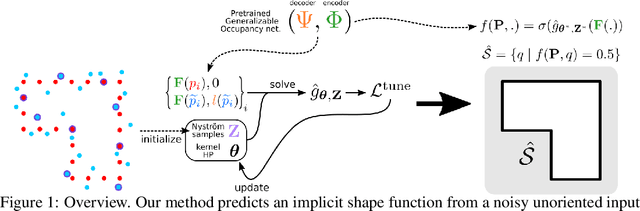
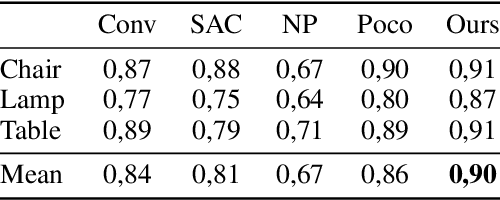
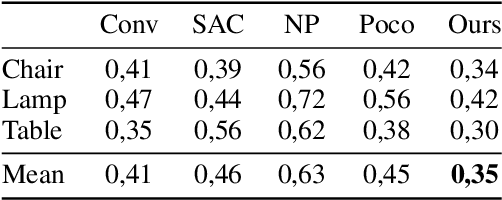
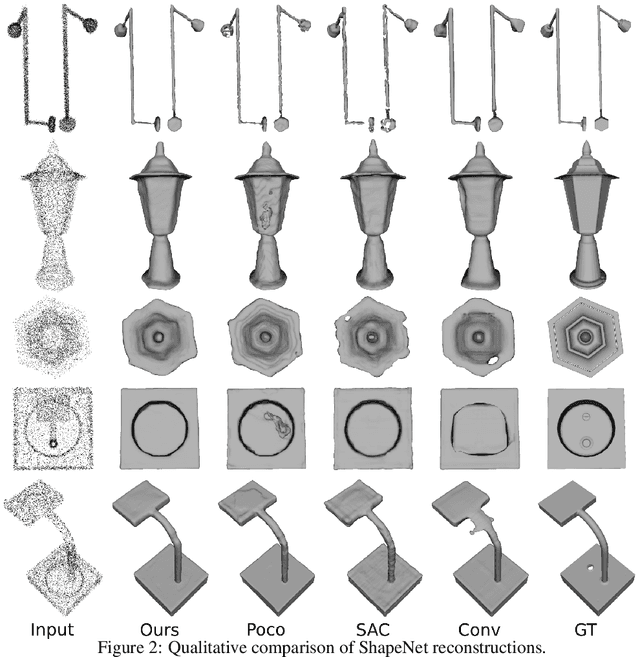
Abstract:Feedforward generalizable models for implicit shape reconstruction from unoriented point cloud present multiple advantages, including high performance and inference speed. However, they still suffer from generalization issues, ranging from underfitting the input point cloud, to misrepresenting samples outside of the training data distribution, or with toplogies unseen at training. We propose here an efficient mechanism to remedy some of these limitations at test time. We combine the inter-shape data prior of the network with an intra-shape regularization prior of a Nystr\"om Kernel Ridge Regression, that we further adapt by fitting its hyperprameters to the current shape. The resulting shape function defined in a shape specific Reproducing Kernel Hilbert Space benefits from desirable stability and efficiency properties and grants a shape adaptive expressiveness-robustness trade-off. We demonstrate the improvement obtained through our method with respect to baselines and the state-of-the-art using synthetic and real data.
Mixing-Denoising Generalizable Occupancy Networks
Nov 20, 2023
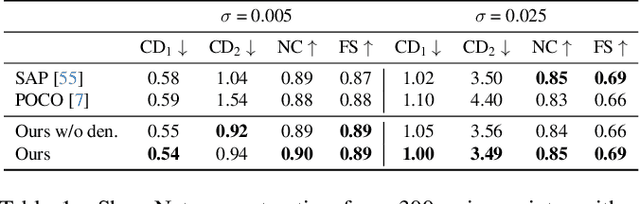
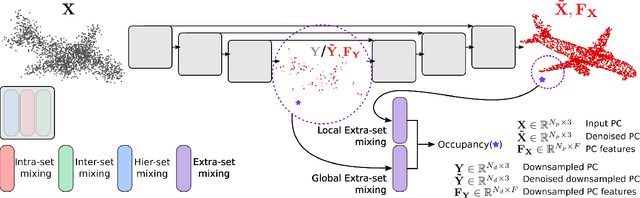
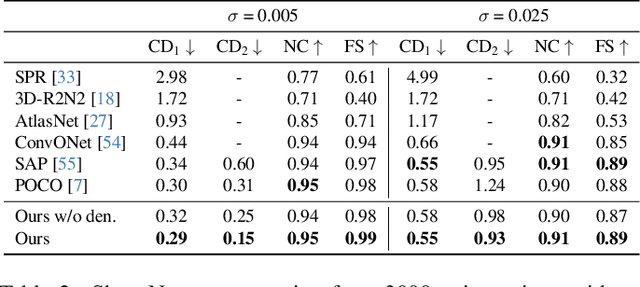
Abstract:While current state-of-the-art generalizable implicit neural shape models rely on the inductive bias of convolutions, it is still not entirely clear how properties emerging from such biases are compatible with the task of 3D reconstruction from point cloud. We explore an alternative approach to generalizability in this context. We relax the intrinsic model bias (i.e. using MLPs to encode local features as opposed to convolutions) and constrain the hypothesis space instead with an auxiliary regularization related to the reconstruction task, i.e. denoising. The resulting model is the first only-MLP locally conditioned implicit shape reconstruction from point cloud network with fast feed forward inference. Point cloud borne features and denoising offsets are predicted from an exclusively MLP-made network in a single forward pass. A decoder predicts occupancy probabilities for queries anywhere in space by pooling nearby features from the point cloud order-invariantly, guided by denoised relative positional encoding. We outperform the state-of-the-art convolutional method while using half the number of model parameters.
Few 'Zero Level Set'-Shot Learning of Shape Signed Distance Functions in Feature Space
Jul 09, 2022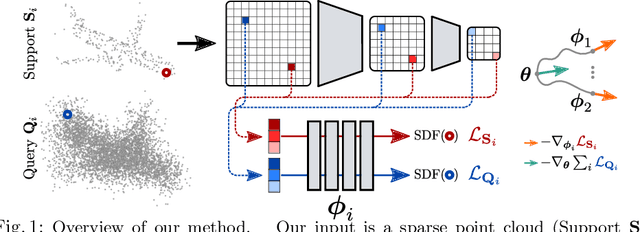



Abstract:We explore a new idea for learning based shape reconstruction from a point cloud, based on the recently popularized implicit neural shape representations. We cast the problem as a few-shot learning of implicit neural signed distance functions in feature space, that we approach using gradient based meta-learning. We use a convolutional encoder to build a feature space given the input point cloud. An implicit decoder learns to predict signed distance values given points represented in this feature space. Setting the input point cloud, i.e. samples from the target shape function's zero level set, as the support (i.e. context) in few-shot learning terms, we train the decoder such that it can adapt its weights to the underlying shape of this context with a few (5) tuning steps. We thus combine two types of implicit neural network conditioning mechanisms simultaneously for the first time, namely feature encoding and meta-learning. Our numerical and qualitative evaluation shows that in the context of implicit reconstruction from a sparse point cloud, our proposed strategy, i.e. meta-learning in feature space, outperforms existing alternatives, namely standard supervised learning in feature space, and meta-learning in euclidean space, while still providing fast inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge