Robustifying Generalizable Implicit Shape Networks with a Tunable Non-Parametric Model
Paper and Code
Nov 21, 2023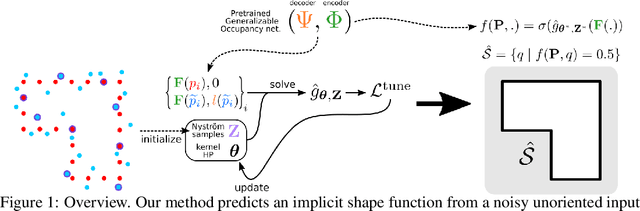
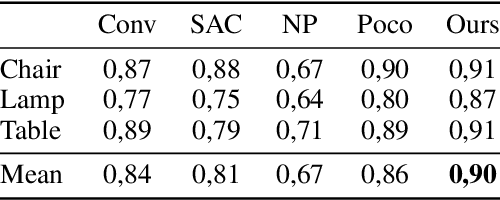
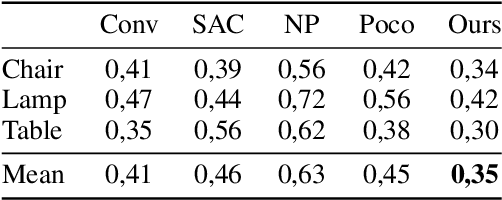
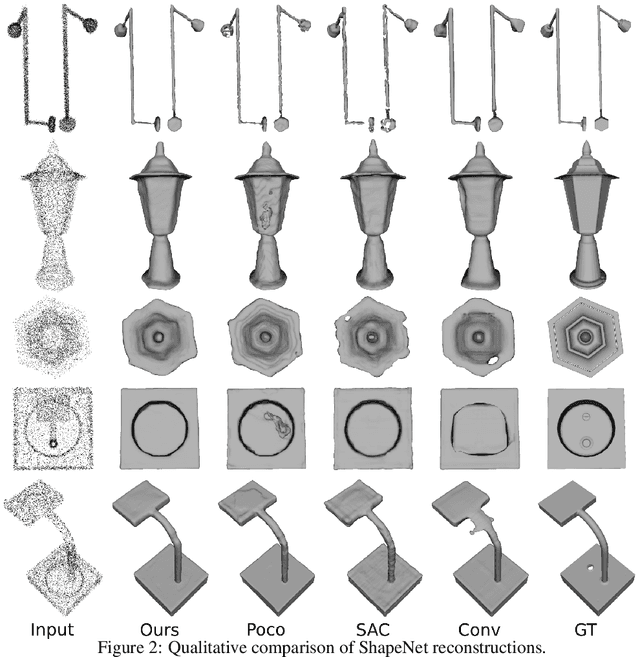
Feedforward generalizable models for implicit shape reconstruction from unoriented point cloud present multiple advantages, including high performance and inference speed. However, they still suffer from generalization issues, ranging from underfitting the input point cloud, to misrepresenting samples outside of the training data distribution, or with toplogies unseen at training. We propose here an efficient mechanism to remedy some of these limitations at test time. We combine the inter-shape data prior of the network with an intra-shape regularization prior of a Nystr\"om Kernel Ridge Regression, that we further adapt by fitting its hyperprameters to the current shape. The resulting shape function defined in a shape specific Reproducing Kernel Hilbert Space benefits from desirable stability and efficiency properties and grants a shape adaptive expressiveness-robustness trade-off. We demonstrate the improvement obtained through our method with respect to baselines and the state-of-the-art using synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge