Toward Robust Neural Reconstruction from Sparse Point Sets
Paper and Code
Dec 20, 2024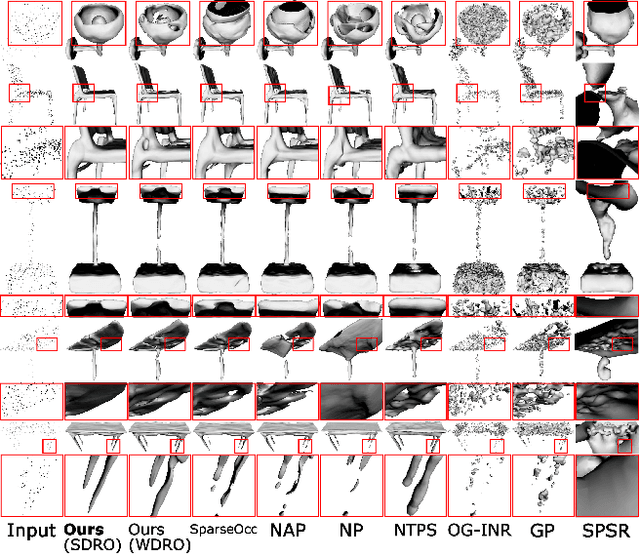
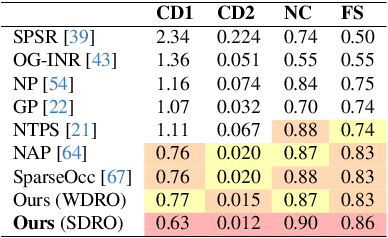
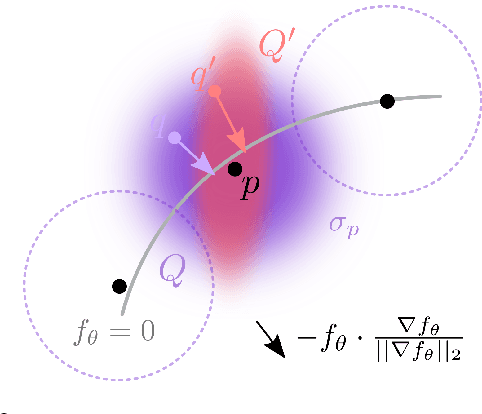
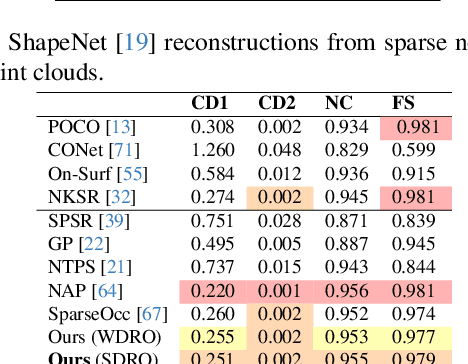
We consider the challenging problem of learning Signed Distance Functions (SDF) from sparse and noisy 3D point clouds. In contrast to recent methods that depend on smoothness priors, our method, rooted in a distributionally robust optimization (DRO) framework, incorporates a regularization term that leverages samples from the uncertainty regions of the model to improve the learned SDFs. Thanks to tractable dual formulations, we show that this framework enables a stable and efficient optimization of SDFs in the absence of ground truth supervision. Using a variety of synthetic and real data evaluations from different modalities, we show that our DRO based learning framework can improve SDF learning with respect to baselines and the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge