Few 'Zero Level Set'-Shot Learning of Shape Signed Distance Functions in Feature Space
Paper and Code
Jul 09, 2022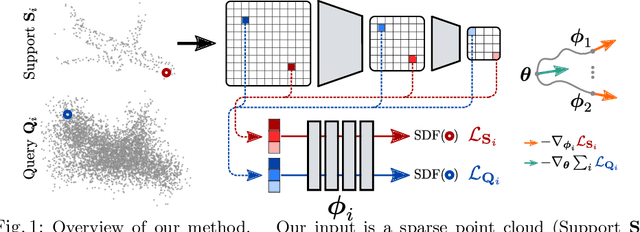



We explore a new idea for learning based shape reconstruction from a point cloud, based on the recently popularized implicit neural shape representations. We cast the problem as a few-shot learning of implicit neural signed distance functions in feature space, that we approach using gradient based meta-learning. We use a convolutional encoder to build a feature space given the input point cloud. An implicit decoder learns to predict signed distance values given points represented in this feature space. Setting the input point cloud, i.e. samples from the target shape function's zero level set, as the support (i.e. context) in few-shot learning terms, we train the decoder such that it can adapt its weights to the underlying shape of this context with a few (5) tuning steps. We thus combine two types of implicit neural network conditioning mechanisms simultaneously for the first time, namely feature encoding and meta-learning. Our numerical and qualitative evaluation shows that in the context of implicit reconstruction from a sparse point cloud, our proposed strategy, i.e. meta-learning in feature space, outperforms existing alternatives, namely standard supervised learning in feature space, and meta-learning in euclidean space, while still providing fast inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge