On the normalized signal to noise ratio in covariance estimation

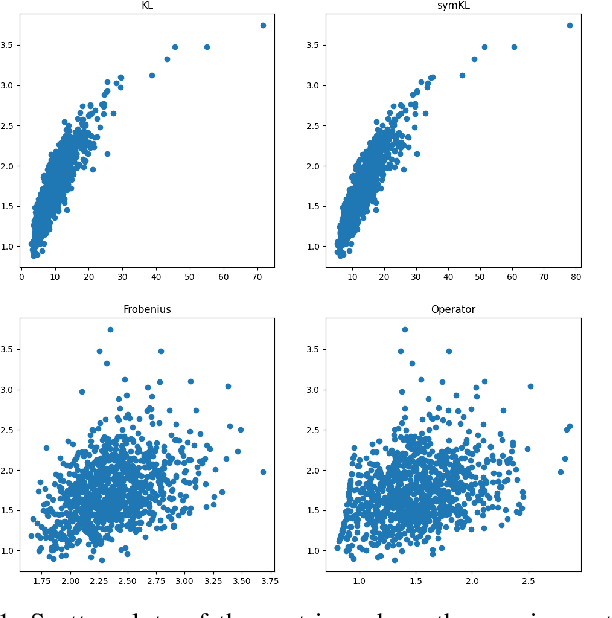
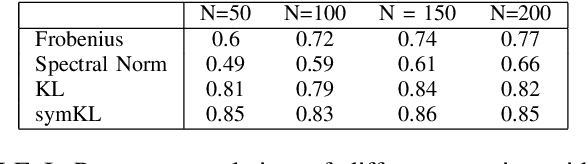
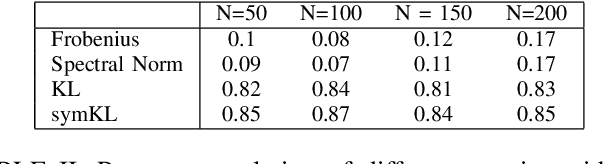
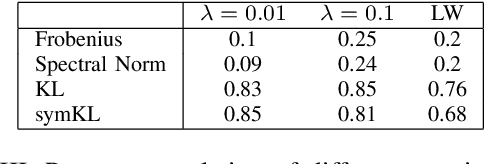
We address the Normalized Signal to Noise Ratio (NSNR) metric defined in the seminal paper by Reed, Mallett and Brennan on adaptive detection. The setting is detection of a target vector in additive correlated noise. NSNR is the ratio between the SNR of a linear detector which uses an estimated noise covariance and the SNR of clairvoyant detector based on the exact unknown covariance. It is not obvious how to evaluate NSNR since it is a function of the target vector. To close this gap, we consider the NSNR associated with the worst target. Using the Kantorovich Inequality, we provide a closed form solution for the worst case NSNR. Then, we prove that the classical Gaussian Kullback Leibler (KL) divergence bounds it. Numerical experiments with different true covariances and various estimates also suggest that the KL metric is more correlated with the NSNR metric than competing norm based metrics.

Learning minimal volume uncertainty ellipsoids

We consider the problem of learning uncertainty regions for parameter estimation problems. The regions are ellipsoids that minimize the average volumes subject to a prescribed coverage probability. As expected, under the assumption of jointly Gaussian data, we prove that the optimal ellipsoid is centered around the conditional mean and shaped as the conditional covariance matrix. In more practical cases, we propose a differentiable optimization approach for approximately computing the optimal ellipsoids using a neural network with proper calibration. Compared to existing methods, our network requires less storage and less computations in inference time, leading to accurate yet smaller ellipsoids. We demonstrate these advantages on four real-world localization datasets.

Self-Supervised Learning for Covariance Estimation

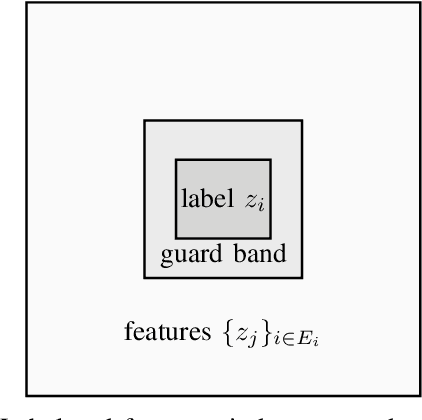
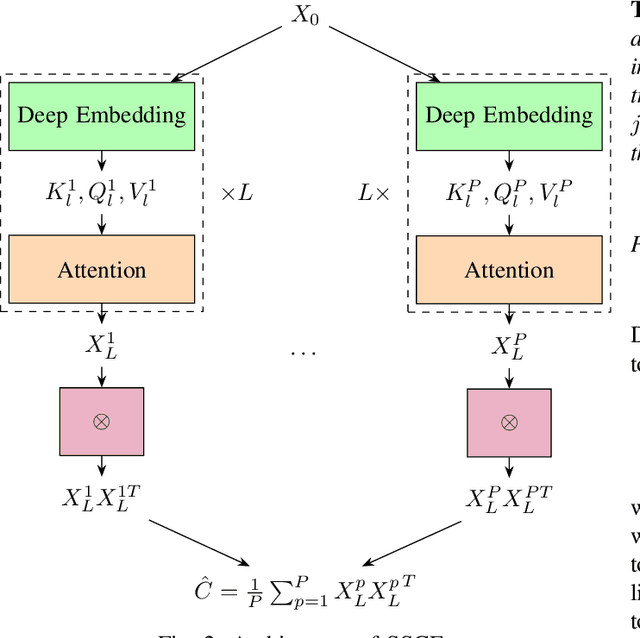
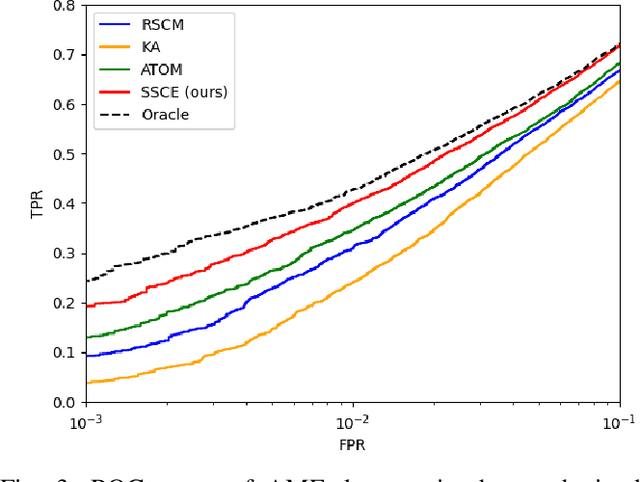
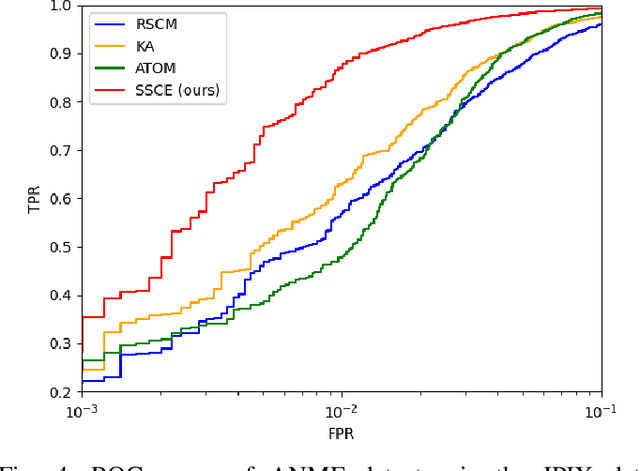
We consider the use of deep learning for covariance estimation. We propose to globally learn a neural network that will then be applied locally at inference time. Leveraging recent advancements in self-supervised foundational models, we train the network without any labeling by simply masking different samples and learning to predict their covariance given their surrounding neighbors. The architecture is based on the popular attention mechanism. Its main advantage over classical methods is the automatic exploitation of global characteristics without any distributional assumptions or regularization. It can be pre-trained as a foundation model and then be repurposed for various downstream tasks, e.g., adaptive target detection in radar or hyperspectral imagery.

Probabilistic Simplex Component Analysis by Importance Sampling

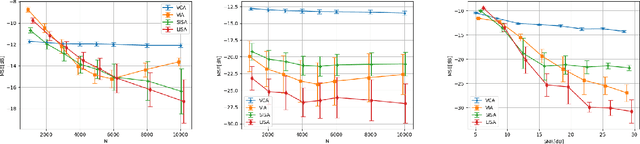
In this paper we consider the problem of linear unmixing hidden random variables defined over the simplex with additive Gaussian noise, also known as probabilistic simplex component analysis (PRISM). Previous solutions to tackle this challenging problem were based on geometrical approaches or computationally intensive variational methods. In contrast, we propose a conventional expectation maximization (EM) algorithm which embeds importance sampling. For this purpose, the proposal distribution is chosen as a simple surrogate distribution of the target posterior that is guaranteed to lie in the simplex. This distribution is based on the Gaussian linear minimum mean squared error (LMMSE) approximation which is accurate at high signal-to-noise ratio. Numerical experiments in different settings demonstrate the advantages of this adaptive surrogate over state-of-the-art methods.

CFARnet: deep learning for target detection with constant false alarm rate

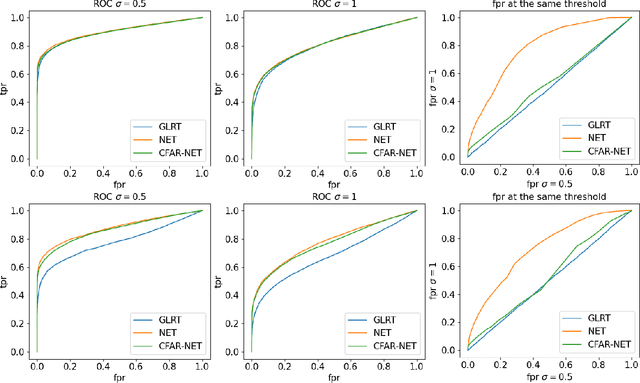
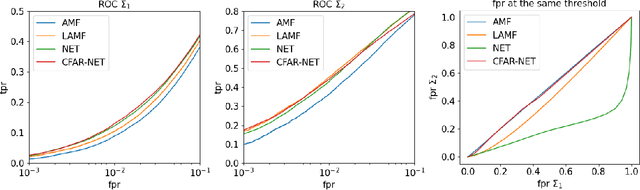
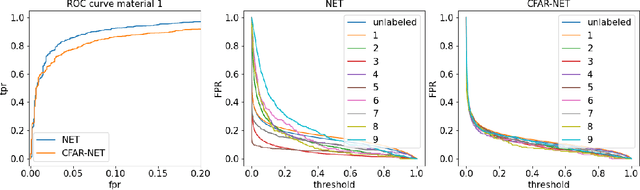
We consider the problem of learning detectors with a Constant False Alarm Rate (CFAR). Classical model-based solutions to composite hypothesis testing are sensitive to imperfect models and are often computationally expensive. In contrast, data-driven machine learning is often more robust and yields classifiers with fixed computational complexity. Learned detectors usually do not have a CFAR as required in many applications. To close this gap, we introduce CFARnet where the loss function is penalized to promote similar distributions of the detector under any null hypothesis scenario. Asymptotic analysis in the case of linear models with general Gaussian noise reveals that the classical generalized likelihood ratio test (GLRT) is actually a minimizer of the CFAR constrained Bayes risk. Experiments in both synthetic data and real hyper-spectral images show that CFARnet leads to near CFAR detectors with similar accuracy as their competitors.

Learning to Detect with Constant False Alarm Rate

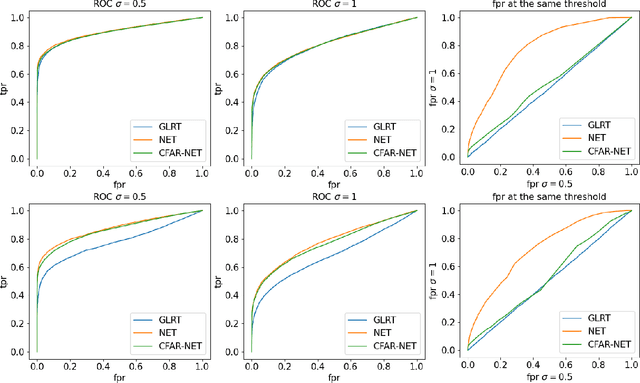
We consider the use of machine learning for hypothesis testing with an emphasis on target detection. Classical model-based solutions rely on comparing likelihoods. These are sensitive to imperfect models and are often computationally expensive. In contrast, data-driven machine learning is often more robust and yields classifiers with fixed computational complexity. Learned detectors usually provide high accuracy with low complexity but do not have a constant false alarm rate (CFAR) as required in many applications. To close this gap, we propose to add a term to the loss function that promotes similar distributions of the detector under any null hypothesis scenario. Experiments show that our approach leads to near CFAR detectors with similar accuracy as their competitors.

On the Optimization Landscape of Maximum Mean Discrepancy

Generative models have been successfully used for generating realistic signals. Because the likelihood function is typically intractable in most of these models, the common practice is to use "implicit" models that avoid likelihood calculation. However, it is hard to obtain theoretical guarantees for such models. In particular, it is not understood when they can globally optimize their non-convex objectives. Here we provide such an analysis for the case of Maximum Mean Discrepancy (MMD) learning of generative models. We prove several optimality results, including for a Gaussian distribution with low rank covariance (where likelihood is inapplicable) and a mixture of Gaussians. Our analysis shows that that the MMD optimization landscape is benign in these cases, and therefore gradient based methods will globally minimize the MMD objective.

Learning to Estimate Without Bias

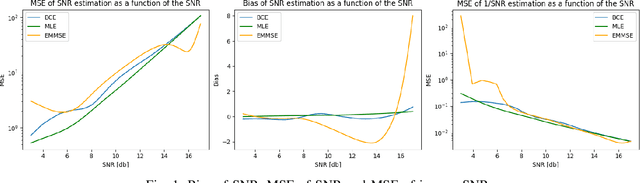
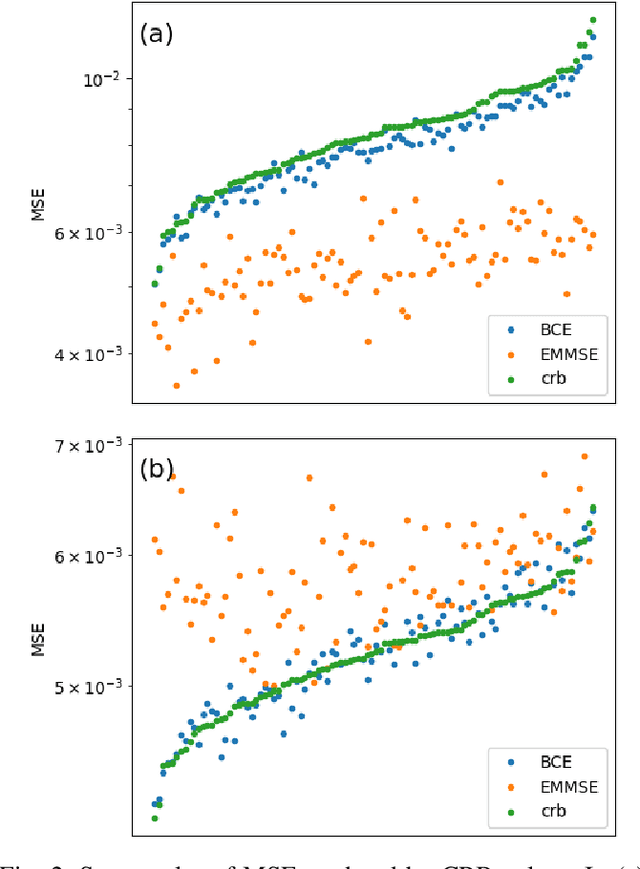
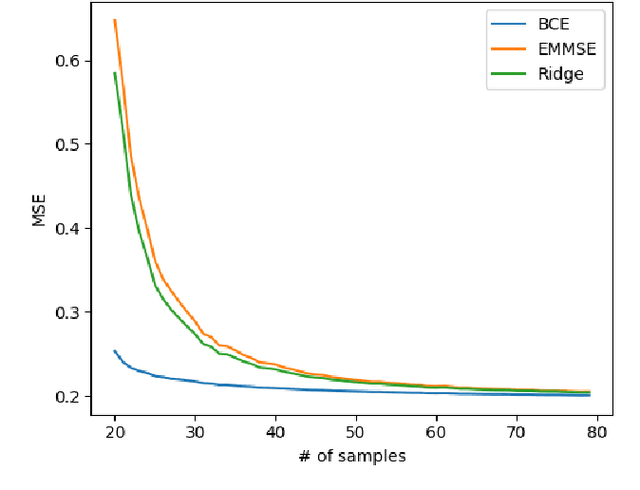
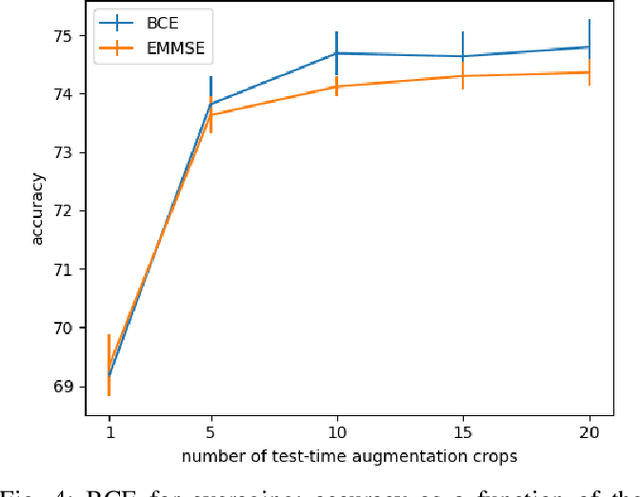
We consider the use of deep learning for parameter estimation. We propose Bias Constrained Estimators (BCE) that add a squared bias term to the standard mean squared error (MSE) loss. The main motivation to BCE is learning to estimate deterministic unknown parameters with no Bayesian prior. Unlike standard learning based estimators that are optimal on average, we prove that BCEs converge to Minimum Variance Unbiased Estimators (MVUEs). We derive closed form solutions to linear BCEs. These provide a flexible bridge between linear regrssion and the least squares method. In non-linear settings, we demonstrate that BCEs perform similarly to MVUEs even when the latter are computationally intractable. A second motivation to BCE is in applications where multiple estimates of the same unknown are averaged for improved performance. Examples include distributed sensor networks and data augmentation in test-time. In such applications, unbiasedness is a necessary condition for asymptotic consistency.

Conditional Frechet Inception Distance

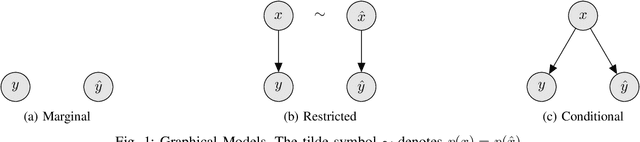
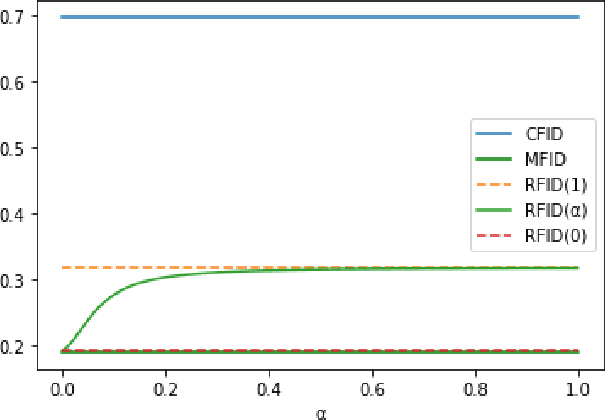
We consider distance functions between conditional distributions functions. We focus on the Wasserstein metric and its Gaussian case known as the Frechet Inception Distance (FID).We develop conditional versions of these metrics, and analyze their relations. Then, we numerically compare the metrics inthe context of performance evaluation of conditional generative models. Our results show that the metrics are similar in classical models which are less susceptible to conditional collapse. But the conditional distances are more informative in modern unsuper-vised, semisupervised and unpaired models where learning the relations between the inputs and outputs is the main challenge.

Maximin Optimization for Binary Regression

We consider regression problems with binary weights. Such optimization problems are ubiquitous in quantized learning models and digital communication systems. A natural approach is to optimize the corresponding Lagrangian using variants of the gradient ascent-descent method. Such maximin techniques are still poorly understood even in the concave-convex case. The non-convex binary constraints may lead to spurious local minima. Interestingly, we prove that this approach is optimal in linear regression with low noise conditions as well as robust regression with a small number of outliers. Practically, the method also performs well in regression with cross entropy loss, as well as non-convex multi-layer neural networks. Taken together our approach highlights the potential of saddle-point optimization for learning constrained models.