CFARnet: deep learning for target detection with constant false alarm rate
Paper and Code
Aug 04, 2022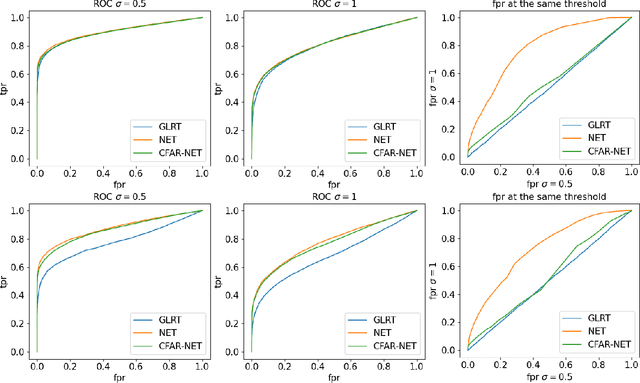
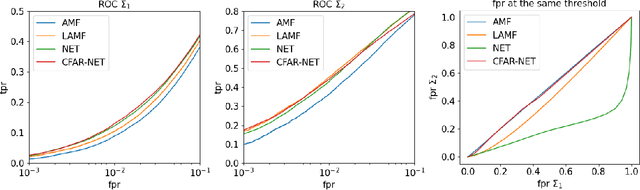

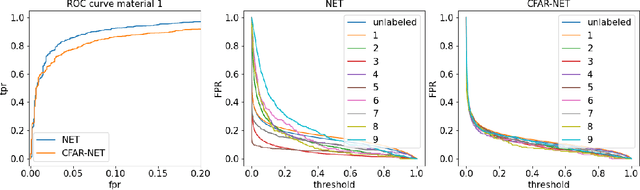
We consider the problem of learning detectors with a Constant False Alarm Rate (CFAR). Classical model-based solutions to composite hypothesis testing are sensitive to imperfect models and are often computationally expensive. In contrast, data-driven machine learning is often more robust and yields classifiers with fixed computational complexity. Learned detectors usually do not have a CFAR as required in many applications. To close this gap, we introduce CFARnet where the loss function is penalized to promote similar distributions of the detector under any null hypothesis scenario. Asymptotic analysis in the case of linear models with general Gaussian noise reveals that the classical generalized likelihood ratio test (GLRT) is actually a minimizer of the CFAR constrained Bayes risk. Experiments in both synthetic data and real hyper-spectral images show that CFARnet leads to near CFAR detectors with similar accuracy as their competitors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge