Overcomplete Independent Component Analysis via SDP

We present a novel algorithm for overcomplete independent components analysis (ICA), where the number of latent sources k exceeds the dimension p of observed variables. Previous algorithms either suffer from high computational complexity or make strong assumptions about the form of the mixing matrix. Our algorithm does not make any sparsity assumption yet enjoys favorable computational and theoretical properties. Our algorithm consists of two main steps: (a) estimation of the Hessians of the cumulant generating function (as opposed to the fourth and higher order cumulants used by most algorithms) and (b) a novel semi-definite programming (SDP) relaxation for recovering a mixing component. We show that this relaxation can be efficiently solved with a projected accelerated gradient descent method, which makes the whole algorithm computationally practical. Moreover, we conjecture that the proposed program recovers a mixing component at the rate k < p^2/4 and prove that a mixing component can be recovered with high probability when k < (2 - epsilon) p log p when the original components are sampled uniformly at random on the hyper sphere. Experiments are provided on synthetic data and the CIFAR-10 dataset of real images.

Optimality and Sub-optimality of PCA I: Spiked Random Matrix Models

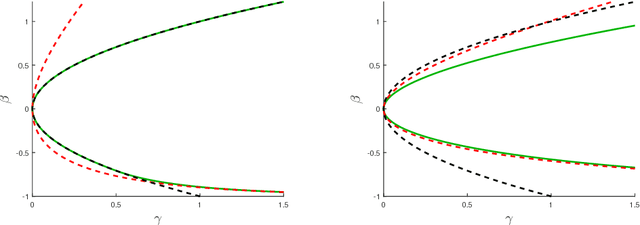
A central problem of random matrix theory is to understand the eigenvalues of spiked random matrix models, introduced by Johnstone, in which a prominent eigenvector (or "spike") is planted into a random matrix. These distributions form natural statistical models for principal component analysis (PCA) problems throughout the sciences. Baik, Ben Arous and Peche showed that the spiked Wishart ensemble exhibits a sharp phase transition asymptotically: when the spike strength is above a critical threshold, it is possible to detect the presence of a spike based on the top eigenvalue, and below the threshold the top eigenvalue provides no information. Such results form the basis of our understanding of when PCA can detect a low-rank signal in the presence of noise. However, under structural assumptions on the spike, not all information is necessarily contained in the spectrum. We study the statistical limits of tests for the presence of a spike, including non-spectral tests. Our results leverage Le Cam's notion of contiguity, and include: i) For the Gaussian Wigner ensemble, we show that PCA achieves the optimal detection threshold for certain natural priors for the spike. ii) For any non-Gaussian Wigner ensemble, PCA is sub-optimal for detection. However, an efficient variant of PCA achieves the optimal threshold (for natural priors) by pre-transforming the matrix entries. iii) For the Gaussian Wishart ensemble, the PCA threshold is optimal for positive spikes (for natural priors) but this is not always the case for negative spikes.

Notes on computational-to-statistical gaps: predictions using statistical physics

In these notes we describe heuristics to predict computational-to-statistical gaps in certain statistical problems. These are regimes in which the underlying statistical problem is information-theoretically possible although no efficient algorithm exists, rendering the problem essentially unsolvable for large instances. The methods we describe here are based on mature, albeit non-rigorous, tools from statistical physics. These notes are based on a lecture series given by the authors at the Courant Institute of Mathematical Sciences in New York City, on May 16th, 2017.

Statistical limits of spiked tensor models

We study the statistical limits of both detecting and estimating a rank-one deformation of a symmetric random Gaussian tensor. We establish upper and lower bounds on the critical signal-to-noise ratio, under a variety of priors for the planted vector: (i) a uniformly sampled unit vector, (ii) i.i.d. $\pm 1$ entries, and (iii) a sparse vector where a constant fraction $\rho$ of entries are i.i.d. $\pm 1$ and the rest are zero. For each of these cases, our upper and lower bounds match up to a $1+o(1)$ factor as the order $d$ of the tensor becomes large. For sparse signals (iii), our bounds are also asymptotically tight in the sparse limit $\rho \to 0$ for any fixed $d$ (including the $d=2$ case of sparse PCA). Our upper bounds for (i) demonstrate a phenomenon reminiscent of the work of Baik, Ben Arous and P\'ech\'e: an `eigenvalue' of a perturbed tensor emerges from the bulk at a strictly lower signal-to-noise ratio than when the perturbation itself exceeds the bulk; we quantify the size of this effect. We also provide some general results for larger classes of priors. In particular, the large $d$ asymptotics of the threshold location differs between problems with discrete priors versus continuous priors. Finally, for priors (i) and (ii) we carry out the replica prediction from statistical physics, which is conjectured to give the exact information-theoretic threshold for any fixed $d$. Of independent interest, we introduce a new improvement to the second moment method for contiguity, on which our lower bounds are based. Our technique conditions away from rare `bad' events that depend on interactions between the signal and noise. This enables us to close $\sqrt{2}$-factor gaps present in several previous works.

Optimality and Sub-optimality of PCA for Spiked Random Matrices and Synchronization

A central problem of random matrix theory is to understand the eigenvalues of spiked random matrix models, in which a prominent eigenvector is planted into a random matrix. These distributions form natural statistical models for principal component analysis (PCA) problems throughout the sciences. Baik, Ben Arous and P\'ech\'e showed that the spiked Wishart ensemble exhibits a sharp phase transition asymptotically: when the signal strength is above a critical threshold, it is possible to detect the presence of a spike based on the top eigenvalue, and below the threshold the top eigenvalue provides no information. Such results form the basis of our understanding of when PCA can detect a low-rank signal in the presence of noise. However, not all the information about the spike is necessarily contained in the spectrum. We study the fundamental limitations of statistical methods, including non-spectral ones. Our results include: I) For the Gaussian Wigner ensemble, we show that PCA achieves the optimal detection threshold for a variety of benign priors for the spike. We extend previous work on the spherically symmetric and i.i.d. Rademacher priors through an elementary, unified analysis. II) For any non-Gaussian Wigner ensemble, we show that PCA is always suboptimal for detection. However, a variant of PCA achieves the optimal threshold (for benign priors) by pre-transforming the matrix entries according to a carefully designed function. This approach has been stated before, and we give a rigorous and general analysis. III) For both the Gaussian Wishart ensemble and various synchronization problems over groups, we show that inefficient procedures can work below the threshold where PCA succeeds, whereas no known efficient algorithm achieves this. This conjectural gap between what is statistically possible and what can be done efficiently remains open.

A semidefinite program for unbalanced multisection in the stochastic block model

We propose a semidefinite programming (SDP) algorithm for community detection in the stochastic block model, a popular model for networks with latent community structure. We prove that our algorithm achieves exact recovery of the latent communities, up to the information-theoretic limits determined by Abbe and Sandon (2015). Our result extends prior SDP approaches by allowing for many communities of different sizes. By virtue of a semidefinite approach, our algorithms succeed against a semirandom variant of the stochastic block model, guaranteeing a form of robustness and generalization. We further explore how semirandom models can lend insight into both the strengths and limitations of SDPs in this setting.

Message-passing algorithms for synchronization problems over compact groups

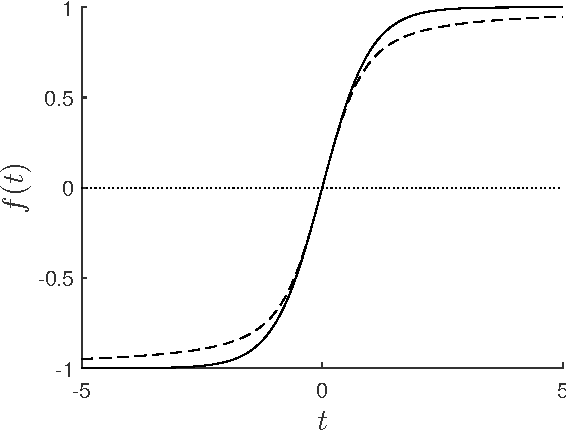
Various alignment problems arising in cryo-electron microscopy, community detection, time synchronization, computer vision, and other fields fall into a common framework of synchronization problems over compact groups such as Z/L, U(1), or SO(3). The goal of such problems is to estimate an unknown vector of group elements given noisy relative observations. We present an efficient iterative algorithm to solve a large class of these problems, allowing for any compact group, with measurements on multiple 'frequency channels' (Fourier modes, or more generally, irreducible representations of the group). Our algorithm is a highly efficient iterative method following the blueprint of approximate message passing (AMP), which has recently arisen as a central technique for inference problems such as structured low-rank estimation and compressed sensing. We augment the standard ideas of AMP with ideas from representation theory so that the algorithm can work with distributions over compact groups. Using standard but non-rigorous methods from statistical physics we analyze the behavior of our algorithm on a Gaussian noise model, identifying phases where the problem is easy, (computationally) hard, and (statistically) impossible. In particular, such evidence predicts that our algorithm is information-theoretically optimal in many cases, and that the remaining cases show evidence of statistical-to-computational gaps.