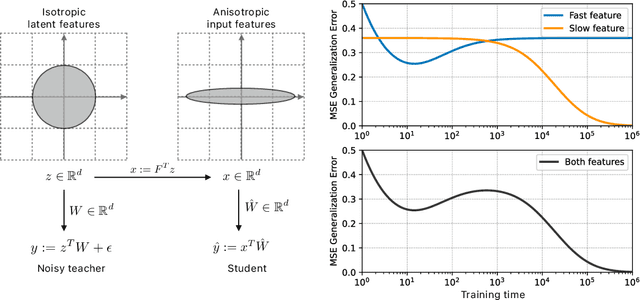
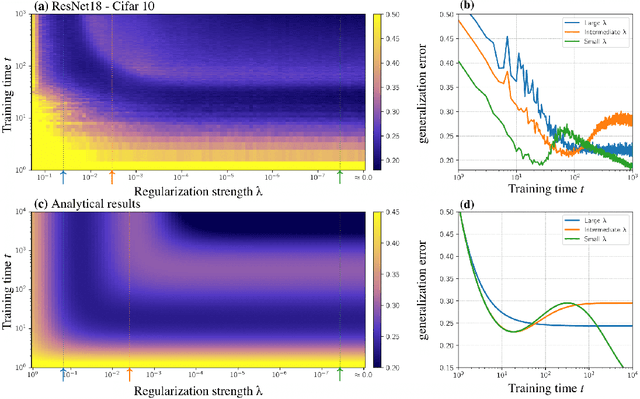
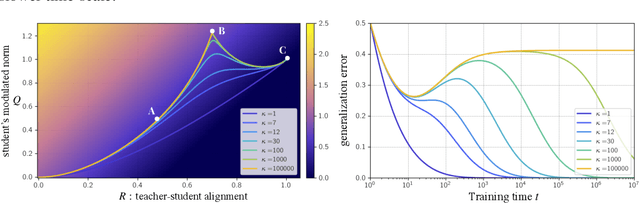
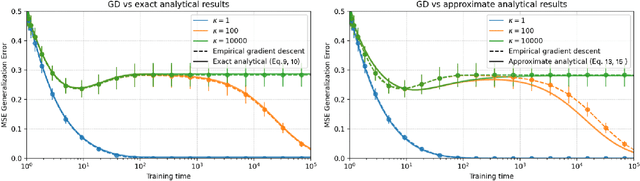
Multi-scale Feature Learning Dynamics: Insights for Double Descent

A key challenge in building theoretical foundations for deep learning is the complex optimization dynamics of neural networks, resulting from the high-dimensional interactions between the large number of network parameters. Such non-trivial dynamics lead to intriguing behaviors such as the phenomenon of "double descent" of the generalization error. The more commonly studied aspect of this phenomenon corresponds to model-wise double descent where the test error exhibits a second descent with increasing model complexity, beyond the classical U-shaped error curve. In this work, we investigate the origins of the less studied epoch-wise double descent in which the test error undergoes two non-monotonous transitions, or descents as the training time increases. By leveraging tools from statistical physics, we study a linear teacher-student setup exhibiting epoch-wise double descent similar to that in deep neural networks. In this setting, we derive closed-form analytical expressions for the evolution of generalization error over training. We find that double descent can be attributed to distinct features being learned at different scales: as fast-learning features overfit, slower-learning features start to fit, resulting in a second descent in test error. We validate our findings through numerical experiments where our theory accurately predicts empirical findings and remains consistent with observations in deep neural networks.

LEAD: Least-Action Dynamics for Min-Max Optimization

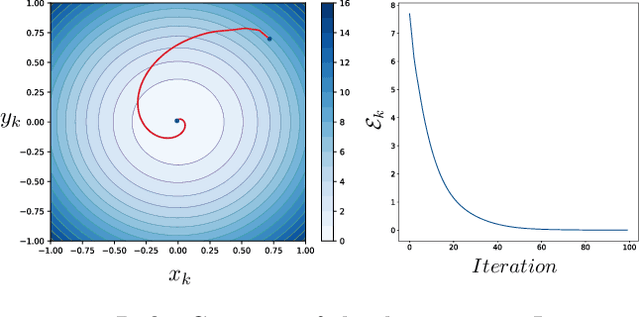
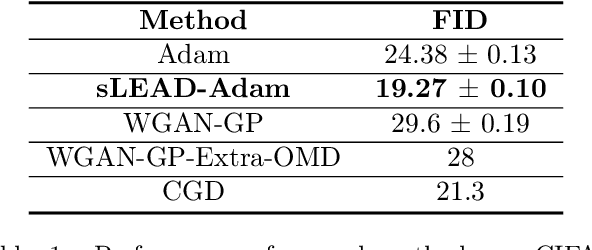
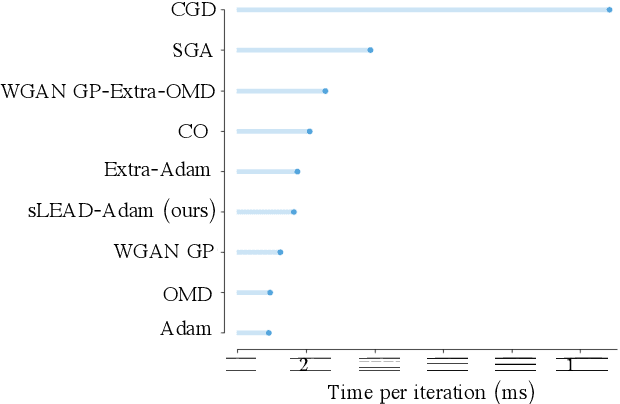
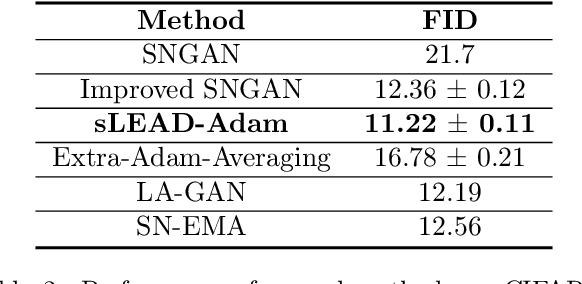
Adversarial formulations in machine learning have rekindled interest in differentiable games. The development of efficient optimization methods for two-player min-max games is an active area of research with a timely impact on adversarial formulations including generative adversarial networks (GANs). Existing methods for this type of problem typically employ intuitive, carefully hand-designed mechanisms for controlling the problematic rotational dynamics commonly encountered during optimization. In this work, we take a novel approach to address this issue by casting min-max optimization as a physical system. We propose LEAD (Least-Action Dynamics), a second-order optimizer that uses the principle of least-action from physics to discover an efficient optimizer for min-max games. We subsequently provide convergence analysis of our optimizer in quadratic min-max games using the Lyapunov theory. Finally, we empirically test our method on synthetic problems and GANs to demonstrate improvements over baseline methods.