LEAD: Least-Action Dynamics for Min-Max Optimization

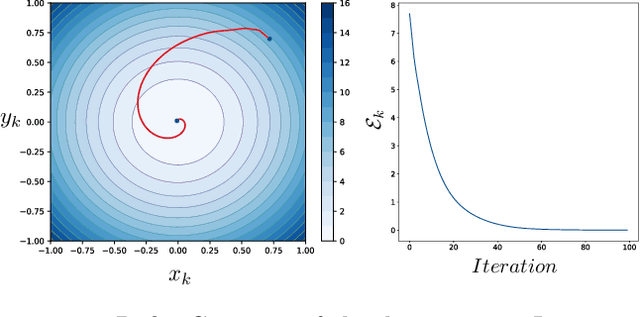
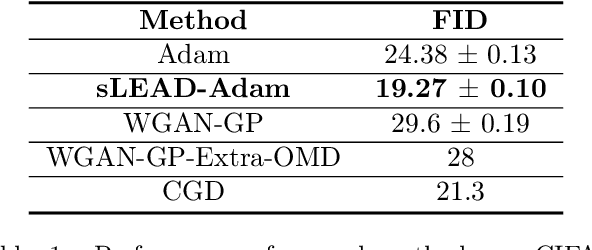
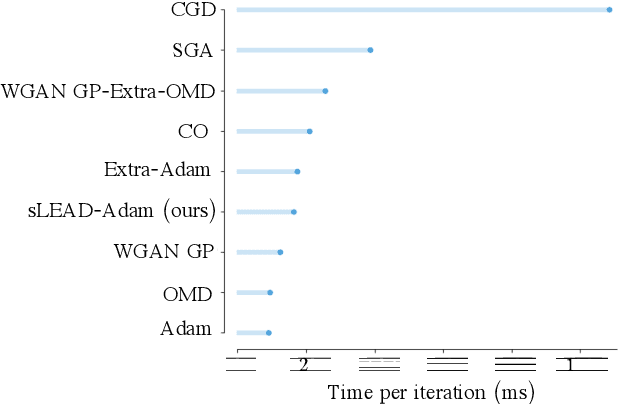
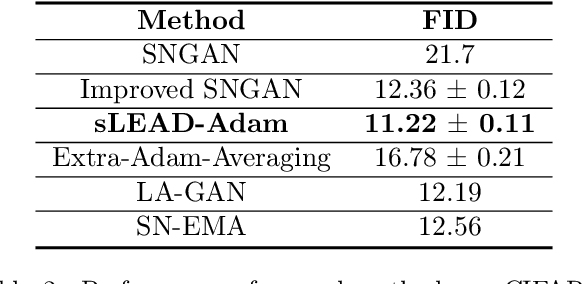
Adversarial formulations in machine learning have rekindled interest in differentiable games. The development of efficient optimization methods for two-player min-max games is an active area of research with a timely impact on adversarial formulations including generative adversarial networks (GANs). Existing methods for this type of problem typically employ intuitive, carefully hand-designed mechanisms for controlling the problematic rotational dynamics commonly encountered during optimization. In this work, we take a novel approach to address this issue by casting min-max optimization as a physical system. We propose LEAD (Least-Action Dynamics), a second-order optimizer that uses the principle of least-action from physics to discover an efficient optimizer for min-max games. We subsequently provide convergence analysis of our optimizer in quadratic min-max games using the Lyapunov theory. Finally, we empirically test our method on synthetic problems and GANs to demonstrate improvements over baseline methods.