Essential-Web v1.0: 24T tokens of organized web data

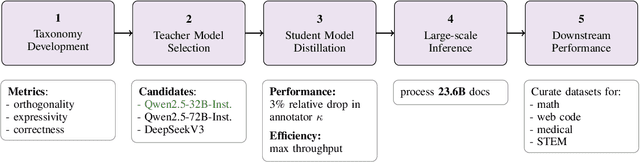
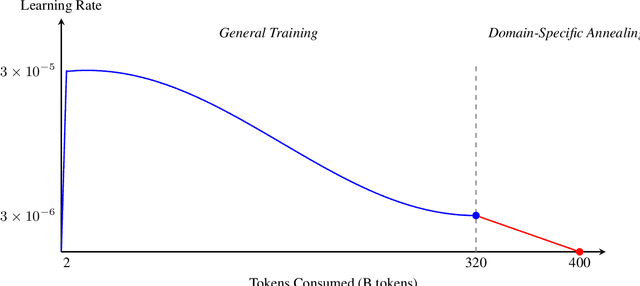
Data plays the most prominent role in how language models acquire skills and knowledge. The lack of massive, well-organized pre-training datasets results in costly and inaccessible data pipelines. We present Essential-Web v1.0, a 24-trillion-token dataset in which every document is annotated with a twelve-category taxonomy covering topic, format, content complexity, and quality. Taxonomy labels are produced by EAI-Distill-0.5b, a fine-tuned 0.5b-parameter model that achieves an annotator agreement within 3% of Qwen2.5-32B-Instruct. With nothing more than SQL-style filters, we obtain competitive web-curated datasets in math (-8.0% relative to SOTA), web code (+14.3%), STEM (+24.5%) and medical (+8.6%). Essential-Web v1.0 is available on HuggingFace: https://huggingface.co/datasets/EssentialAI/essential-web-v1.0

Scaling Graph Neural Networks for Particle Track Reconstruction

Particle track reconstruction is an important problem in high-energy physics (HEP), necessary to study properties of subatomic particles. Traditional track reconstruction algorithms scale poorly with the number of particles within the accelerator. The Exa.TrkX project, to alleviate this computational burden, introduces a pipeline that reduces particle track reconstruction to edge classification on a graph, and uses graph neural networks (GNNs) to produce particle tracks. However, this GNN-based approach is memory-prohibitive and skips graphs that would exceed GPU memory. We introduce improvements to the Exa.TrkX pipeline to train on samples of input particle graphs, and show that these improvements generalize to higher precision and recall. In addition, we adapt performance optimizations, introduced for GNN training, to fit our augmented Exa.TrkX pipeline. These optimizations provide a $2\times$ speedup over our baseline implementation in PyTorch Geometric.

Sparsity-Aware Communication for Distributed Graph Neural Network Training

Graph Neural Networks (GNNs) are a computationally efficient method to learn embeddings and classifications on graph data. However, GNN training has low computational intensity, making communication costs the bottleneck for scalability. Sparse-matrix dense-matrix multiplication (SpMM) is the core computational operation in full-graph training of GNNs. Previous work parallelizing this operation focused on sparsity-oblivious algorithms, where matrix elements are communicated regardless of the sparsity pattern. This leads to a predictable communication pattern that can be overlapped with computation and enables the use of collective communication operations at the expense of wasting significant bandwidth by communicating unnecessary data. We develop sparsity-aware algorithms that tackle the communication bottlenecks in GNN training with three novel approaches. First, we communicate only the necessary matrix elements. Second, we utilize a graph partitioning model to reorder the matrix and drastically reduce the amount of communicated elements. Finally, we address the high load imbalance in communication with a tailored partitioning model, which minimizes both the total communication volume and the maximum sending volume. We further couple these sparsity-exploiting approaches with a communication-avoiding approach (1.5D parallel SpMM) in which submatrices are replicated to reduce communication. We explore the tradeoffs of these combined optimizations and show up to 14X improvement on 256 GPUs and on some instances reducing communication to almost zero resulting in a communication-free parallel training relative to a popular GNN framework based on communication-oblivious SpMM.

Distributed Matrix-Based Sampling for Graph Neural Network Training

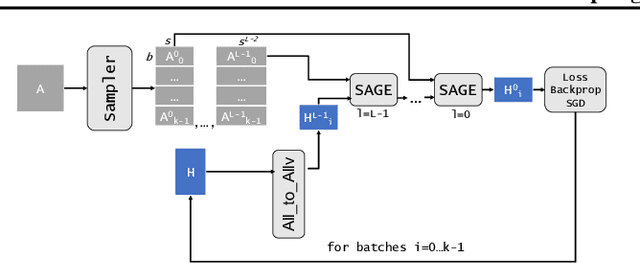
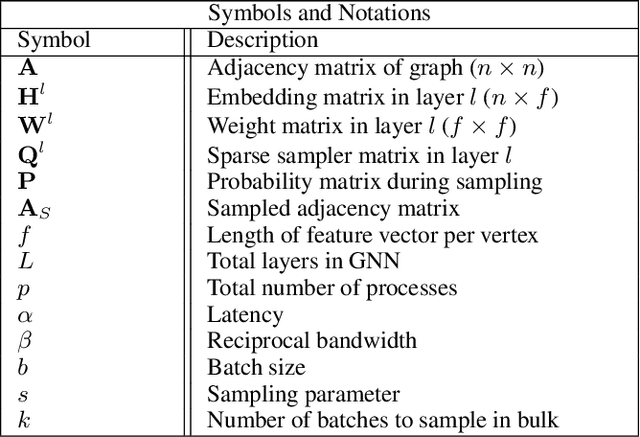
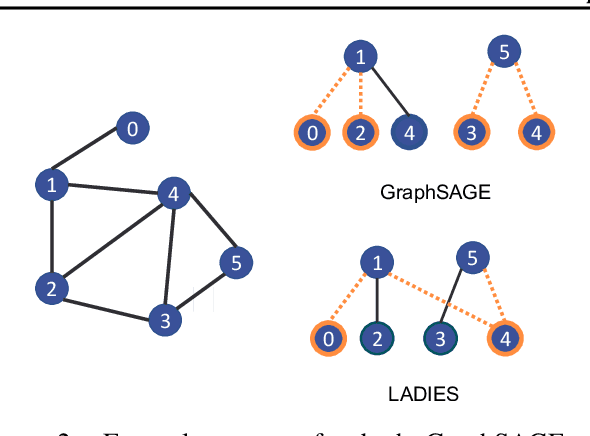
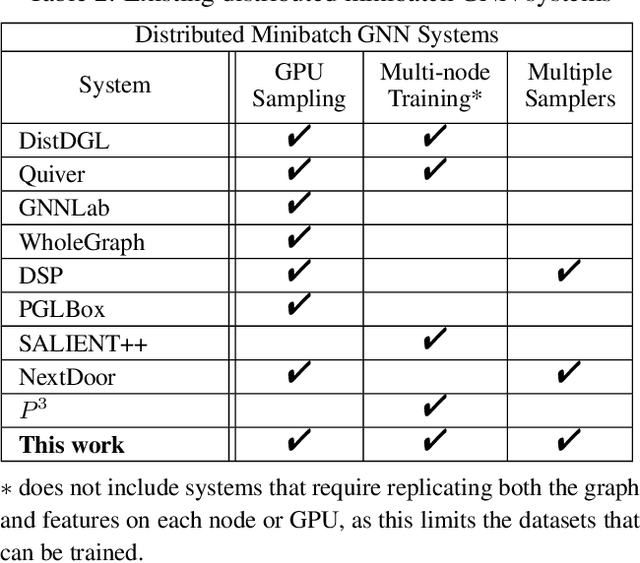
The primary contribution of this paper is new methods for reducing communication in the sampling step for distributed GNN training. Here, we propose a matrix-based bulk sampling approach that expresses sampling as a sparse matrix multiplication (SpGEMM) and samples multiple minibatches at once. When the input graph topology does not fit on a single device, our method distributes the graph and use communication-avoiding SpGEMM algorithms to scale GNN minibatch sampling, enabling GNN training on much larger graphs than those that can fit into a single device memory. When the input graph topology (but not the embeddings) fits in the memory of one GPU, our approach (1) performs sampling without communication, (2) amortizes the overheads of sampling a minibatch, and (3) can represent multiple sampling algorithms by simply using different matrix constructions. In addition to new methods for sampling, we show that judiciously replicating feature data with a simple all-to-all exchange can outperform current methods for the feature extraction step in distributed GNN training. We provide experimental results on the largest Open Graph Benchmark (OGB) datasets on $128$ GPUs, and show that our pipeline is $2.5\times$ faster Quiver (a distributed extension to PyTorch-Geometric) on a $3$-layer GraphSAGE network. On datasets outside of OGB, we show a $8.46\times$ speedup on $128$ GPUs in-per epoch time. Finally, we show scaling when the graph is distributed across GPUs and scaling for both node-wise and layer-wise sampling algorithms

Reducing Communication in Graph Neural Network Training

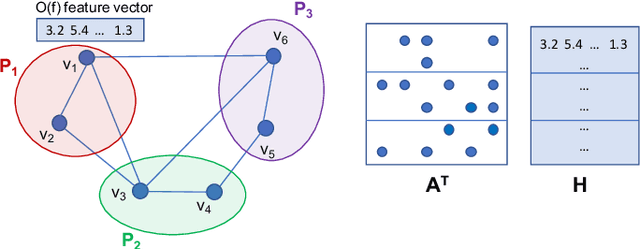
Graph Neural Networks (GNNs) are powerful and flexible neural networks that use the naturally sparse connectivity information of the data. GNNs represent this connectivity as sparse matrices, which have lower arithmetic intensity and thus higher communication costs compared to dense matrices, making GNNs harder to scale to high concurrencies than convolutional or fully-connected neural networks. We present a family of parallel algorithms for training GNNs. These algorithms are based on their counterparts in dense and sparse linear algebra, but they had not been previously applied to GNN training. We show that they can asymptotically reduce communication compared to existing parallel GNN training methods. We implement a promising and practical version that is based on 2D sparse-dense matrix multiplication using torch.distributed. Our implementation parallelizes over GPU-equipped clusters. We train GNNs on up to a hundred GPUs on datasets that include a protein network with over a billion edges.