Sparsity-Aware Communication for Distributed Graph Neural Network Training

Graph Neural Networks (GNNs) are a computationally efficient method to learn embeddings and classifications on graph data. However, GNN training has low computational intensity, making communication costs the bottleneck for scalability. Sparse-matrix dense-matrix multiplication (SpMM) is the core computational operation in full-graph training of GNNs. Previous work parallelizing this operation focused on sparsity-oblivious algorithms, where matrix elements are communicated regardless of the sparsity pattern. This leads to a predictable communication pattern that can be overlapped with computation and enables the use of collective communication operations at the expense of wasting significant bandwidth by communicating unnecessary data. We develop sparsity-aware algorithms that tackle the communication bottlenecks in GNN training with three novel approaches. First, we communicate only the necessary matrix elements. Second, we utilize a graph partitioning model to reorder the matrix and drastically reduce the amount of communicated elements. Finally, we address the high load imbalance in communication with a tailored partitioning model, which minimizes both the total communication volume and the maximum sending volume. We further couple these sparsity-exploiting approaches with a communication-avoiding approach (1.5D parallel SpMM) in which submatrices are replicated to reduce communication. We explore the tradeoffs of these combined optimizations and show up to 14X improvement on 256 GPUs and on some instances reducing communication to almost zero resulting in a communication-free parallel training relative to a popular GNN framework based on communication-oblivious SpMM.

A High-Throughput Solver for Marginalized Graph Kernels on GPU

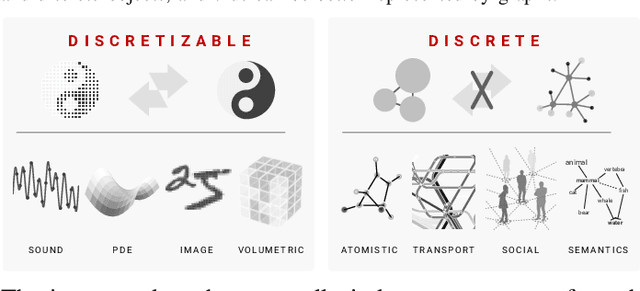
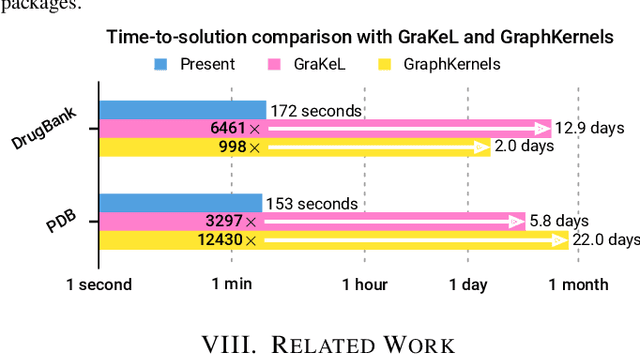
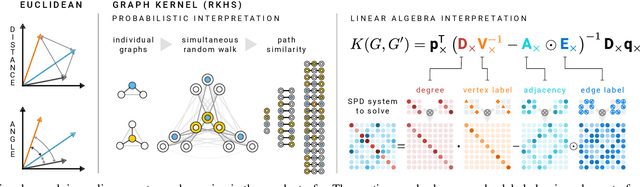
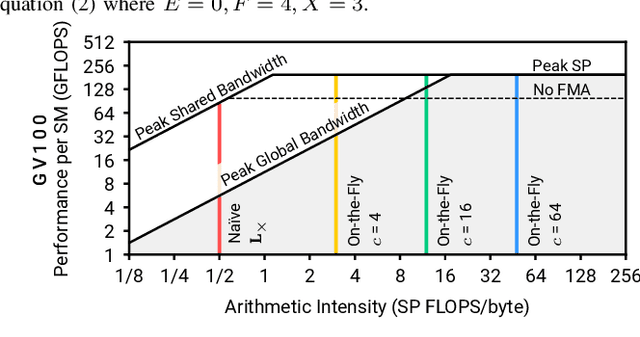
We present the design and optimization of a solver for efficient and high-throughput computation of the marginalized graph kernel on General Purpose GPUs. The graph kernel is computed using the conjugate gradient method to solve a generalized Laplacian of the tensor product between a pair of graphs. To cope with the large gap between the instruction throughput and the memory bandwidth of the GPUs, our solver forms the graph tensor product on-the-fly without storing it in memory. This is achieved by using threads in a warp cooperatively to stream the adjacency and edge label matrices of individual graphs by small square matrix blocks called tiles, which are then staged in registers and the shared memory for later reuse. Warps across a thread block can further share tiles via the shared memory to increase data reuse. We exploit the sparsity of the graphs hierarchically by storing only non-empty tiles using a coordinate format and nonzero elements within each tile using bitmaps. We propose a new partition-based reordering algorithm for aggregating nonzero elements of the graphs into fewer but denser tiles to further exploit sparsity. We carry out extensive theoretical analyses on the graph tensor product primitives for tiles of various density and evaluate their performance on synthetic and real-world datasets. Our solver delivers three to four orders of magnitude speedup over existing CPU-based solvers such as GraKeL and GraphKernels. The capability of the solver enables kernel-based learning tasks at unprecedented scales.