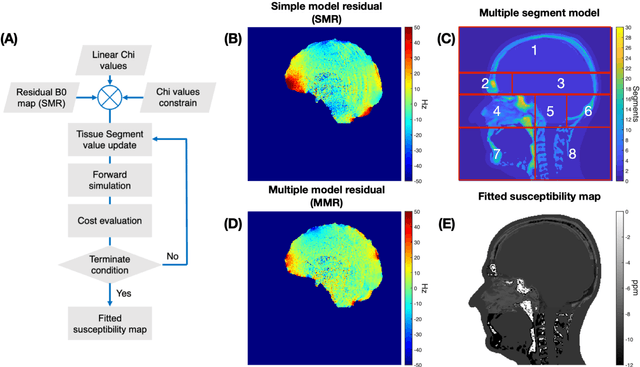
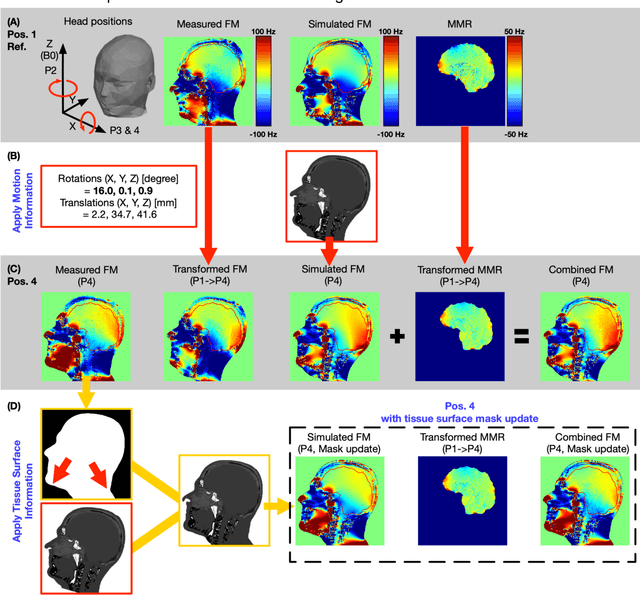
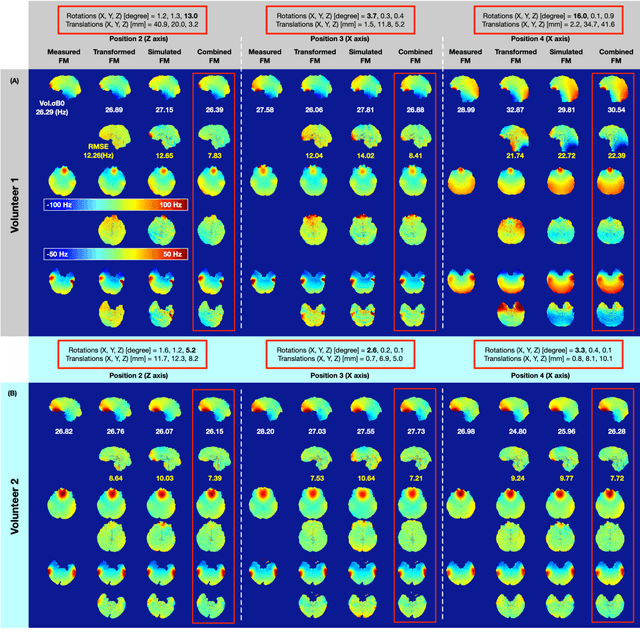
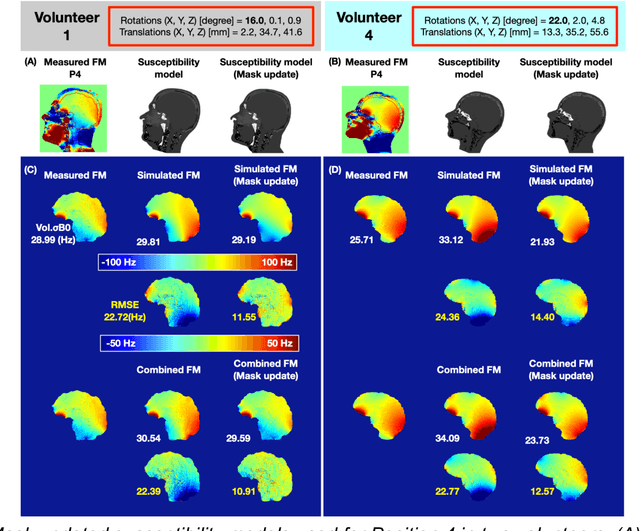
Prediction of motion induced magnetic fields for human brain MRI at 3T

Objective Maps of B0 field inhomogeneities are often used to improve MRI image quality, even in a retrospective fashion. These field inhomogeneities depend on the exact head position within the static field but acquiring field maps (FM) at every position is time consuming. Here we explore different ways to obtain B0 predictions at different head positions. Methods FM were predicted from iterative simulations with four field factors: 1) sample induced B0 field, 2) system's spherical harmonic shim field, 3) perturbing field originating outside the field of view, 4) sequence phase errors. The simulation was improved by including local susceptibility sources estimated from UTE scans and position-specific masks. The estimation performance of the simulated FMs and a transformed FM, obtained from the measured reference FM, were compared with the actual FM at different head positions. Results The transformed FM provided inconsistent results for large head movements (>5 degree rotation), while the simulation strategy had a superior prediction accuracy for all positions. The simulated FM was used to optimize B0 shims with up to 22.2% improvement with respect to the transformed FM approach. Conclusion The proposed simulation strategy is able to predict movement induced B0 field inhomogeneities yielding more precise estimates of the ground truth field homogeneity than the transformed FM.

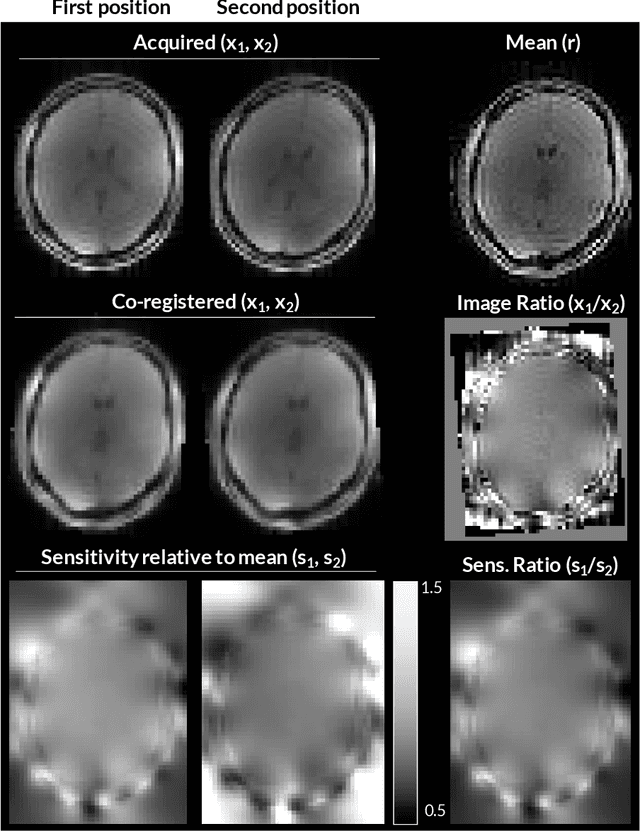
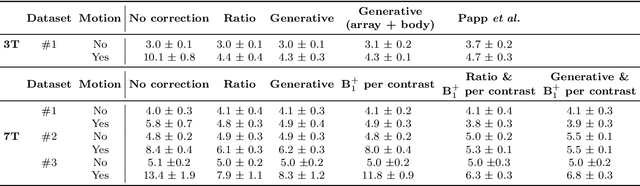
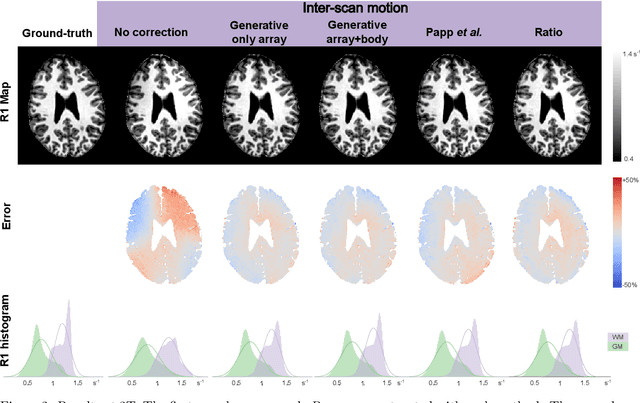
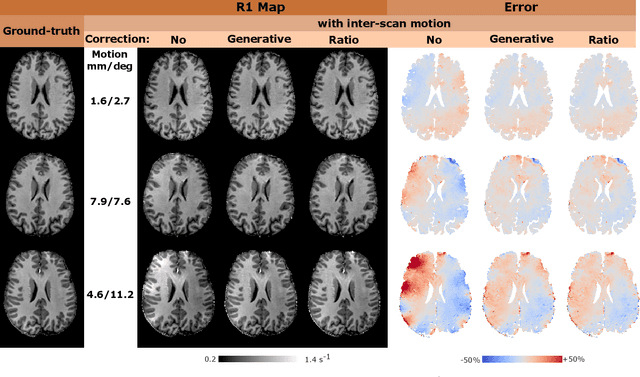
Correcting inter-scan motion artefacts in quantitative R1 mapping at 7T

Purpose: Inter-scan motion is a substantial source of error in $R_1$ estimation, and can be expected to increase at 7T where $B_1$ fields are more inhomogeneous. The established correction scheme does not translate to 7T since it requires a body coil reference. Here we introduce two alternatives that outperform the established method. Since they compute relative sensitivities they do not require body coil images. Theory: The proposed methods use coil-combined magnitude images to obtain the relative coil sensitivities. The first method efficiently computes the relative sensitivities via a simple ratio; the second by fitting a more sophisticated generative model. Methods: $R_1$ maps were computed using the variable flip angle (VFA) approach. Multiple datasets were acquired at 3T and 7T, with and without motion between the acquisition of the VFA volumes. $R_1$ maps were constructed without correction, with the proposed corrections, and (at 3T) with the previously established correction scheme. Results: At 3T, the proposed methods outperform the baseline method. Inter-scan motion artefacts were also reduced at 7T. However, reproducibility only converged on that of the no motion condition if position-specific transmit field effects were also incorporated. Conclusion: The proposed methods simplify inter-scan motion correction of $R_1$ maps and are applicable at both 3T and 7T, where a body coil is typically not available. The open-source code for all methods is made publicly available.