Alfredo Nazabal
Inference and Learning for Generative Capsule Models
Sep 07, 2022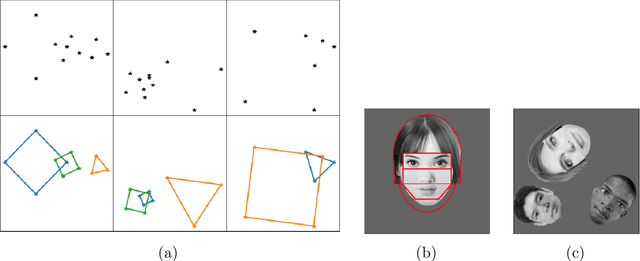
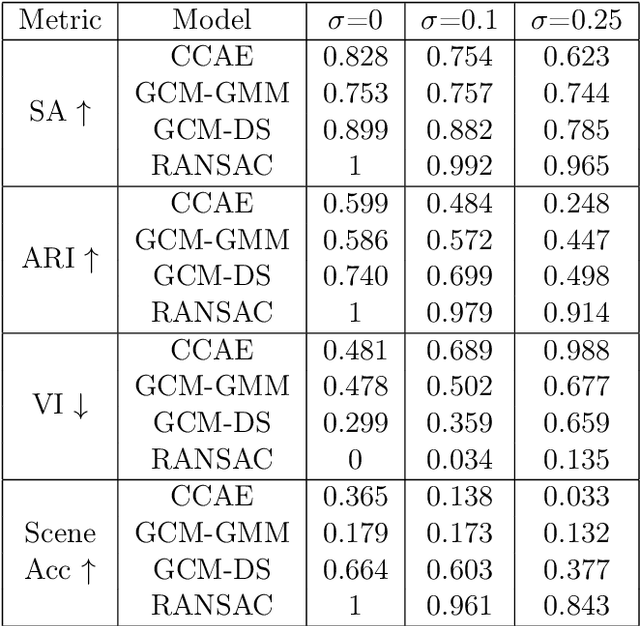

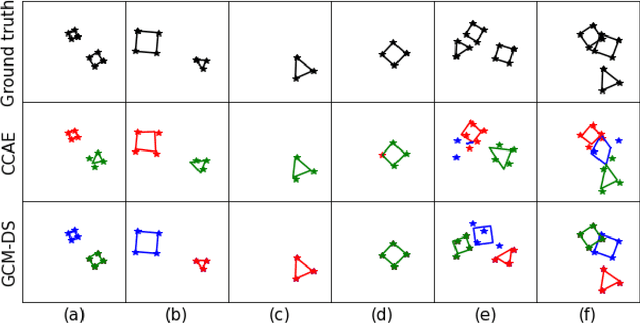
Abstract:Capsule networks (see e.g. Hinton et al., 2018) aim to encode knowledge of and reason about the relationship between an object and its parts. In this paper we specify a generative model for such data, and derive a variational algorithm for inferring the transformation of each model object in a scene, and the assignments of observed parts to the objects. We derive a learning algorithm for the object models, based on variational expectation maximization (Jordan et al., 1999). We also study an alternative inference algorithm based on the RANSAC method of Fischler and Bolles (1981). We apply these inference methods to (i) data generated from multiple geometric objects like squares and triangles ("constellations"), and (ii) data from a parts-based model of faces. Recent work by Kosiorek et al. (2019) has used amortized inference via stacked capsule autoencoders (SCAEs) to tackle this problem -- our results show that we significantly outperform them where we can make comparisons (on the constellations data).
Repairing Systematic Outliers by Learning Clean Subspaces in VAEs
Jul 17, 2022



Abstract:Data cleaning often comprises outlier detection and data repair. Systematic errors result from nearly deterministic transformations that occur repeatedly in the data, e.g. specific image pixels being set to default values or watermarks. Consequently, models with enough capacity easily overfit to these errors, making detection and repair difficult. Seeing as a systematic outlier is a combination of patterns of a clean instance and systematic error patterns, our main insight is that inliers can be modelled by a smaller representation (subspace) in a model than outliers. By exploiting this, we propose Clean Subspace Variational Autoencoder (CLSVAE), a novel semi-supervised model for detection and automated repair of systematic errors. The main idea is to partition the latent space and model inlier and outlier patterns separately. CLSVAE is effective with much less labelled data compared to previous related models, often with less than 2% of the data. We provide experiments using three image datasets in scenarios with different levels of corruption and labelled set sizes, comparing to relevant baselines. CLSVAE provides superior repairs without human intervention, e.g. with just 0.25% of labelled data we see a relative error decrease of 58% compared to the closest baseline.
Inference for Generative Capsule Models
Mar 11, 2021



Abstract:Capsule networks (see e.g. Hinton et al., 2018) aim to encode knowledge and reason about the relationship between an object and its parts. % In this paper we focus on a clean version of this problem, where data is generated from multiple geometric objects (e.g. triangles, squares) at arbitrary translations, rotations and scales, and the observed datapoints (parts) come from the corners of all objects, without any labelling of the objects. We specify a generative model for this data, and derive a variational algorithm for inferring the transformation of each object and the assignments of points to parts of the objects. Recent work by Kosiorek et al. [2019] has used amortized inference via stacked capsule autoencoders (SCA) to tackle this problem -- our results show that we significantly outperform them. We also investigate inference for this problem using a RANSAC-type algorithm.
VAEs in the Presence of Missing Data
Jun 09, 2020



Abstract:Real world datasets often contain entries with missing elements e.g. in a medical dataset, a patient is unlikely to have taken all possible diagnostic tests. Variational Autoencoders (VAEs) are popular generative models often used for unsupervised learning. Despite their widespread use it is unclear how best to apply VAEs to datasets with missing data. We develop a novel latent variable model of a corruption process which generates missing data, and derive a corresponding tractable evidence lower bound (ELBO). Our model is straightforward to implement, can handle both missing completely at random (MCAR) and missing not at random (MNAR) data, scales to high dimensional inputs and gives both the VAE encoder and decoder principled access to indicator variables for whether a data element is missing or not. On the MNIST and SVHN datasets we demonstrate improved marginal log-likelihood of observed data and better missing data imputation, compared to existing approaches.
Handling Incomplete Heterogeneous Data using VAEs
Oct 30, 2018



Abstract:Variational autoencoders (VAEs), as well as other generative models, have been shown to be efficient and accurate to capture the latent structure of vast amounts of complex high-dimensional data. However, existing VAEs can still not directly handle data that are heterogenous (mixed continuous and discrete) or incomplete (with missing data at random), which is indeed common in real-world applications. In this paper, we propose a general framework to design VAEs, suitable for fitting incomplete heterogenous data. The proposed HI-VAE includes likelihood models for real-valued, positive real valued, interval, categorical, ordinal and count data, and allows to estimate (and potentially impute) missing data accurately. Furthermore, HI-VAE presents competitive predictive performance in supervised tasks, outperforming super- vised models when trained on incomplete data
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge