Guide-and-Rescale: Self-Guidance Mechanism for Effective Tuning-Free Real Image Editing

Despite recent advances in large-scale text-to-image generative models, manipulating real images with these models remains a challenging problem. The main limitations of existing editing methods are that they either fail to perform with consistent quality on a wide range of image edits or require time-consuming hyperparameter tuning or fine-tuning of the diffusion model to preserve the image-specific appearance of the input image. We propose a novel approach that is built upon a modified diffusion sampling process via the guidance mechanism. In this work, we explore the self-guidance technique to preserve the overall structure of the input image and its local regions appearance that should not be edited. In particular, we explicitly introduce layout-preserving energy functions that are aimed to save local and global structures of the source image. Additionally, we propose a noise rescaling mechanism that allows to preserve noise distribution by balancing the norms of classifier-free guidance and our proposed guiders during generation. Such a guiding approach does not require fine-tuning the diffusion model and exact inversion process. As a result, the proposed method provides a fast and high-quality editing mechanism. In our experiments, we show through human evaluation and quantitative analysis that the proposed method allows to produce desired editing which is more preferable by humans and also achieves a better trade-off between editing quality and preservation of the original image. Our code is available at https://github.com/FusionBrainLab/Guide-and-Rescale.

Already Moderate Population Sizes Provably Yield Strong Robustness to Noise

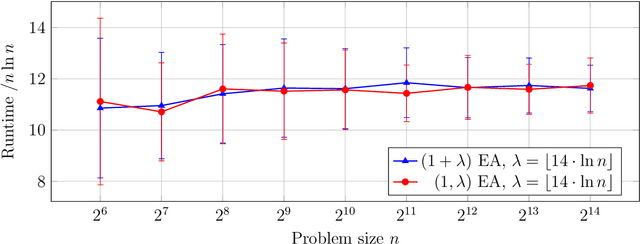
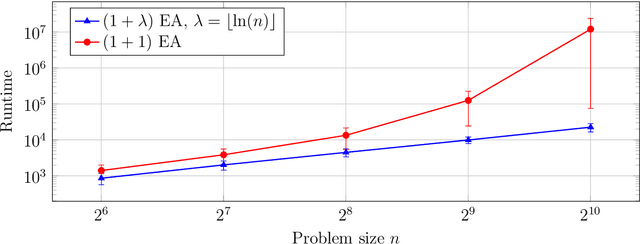
Experience shows that typical evolutionary algorithms can cope well with stochastic disturbances such as noisy function evaluations. In this first mathematical runtime analysis of the $(1+\lambda)$ and $(1,\lambda)$ evolutionary algorithms in the presence of prior bit-wise noise, we show that both algorithms can tolerate constant noise probabilities without increasing the asymptotic runtime on the OneMax benchmark. For this, a population size $\lambda$ suffices that is at least logarithmic in the problem size $n$. The only previous result in this direction regarded the less realistic one-bit noise model, required a population size super-linear in the problem size, and proved a runtime guarantee roughly cubic in the noiseless runtime for the OneMax benchmark. Our significantly stronger results are based on the novel proof argument that the noiseless offspring can be seen as a biased uniform crossover between the parent and the noisy offspring. We are optimistic that the technical lemmas resulting from this insight will find applications also in future mathematical runtime analyses of evolutionary algorithms.

Larger Offspring Populations Help the $(1 + (λ, λ))$ Genetic Algorithm to Overcome the Noise

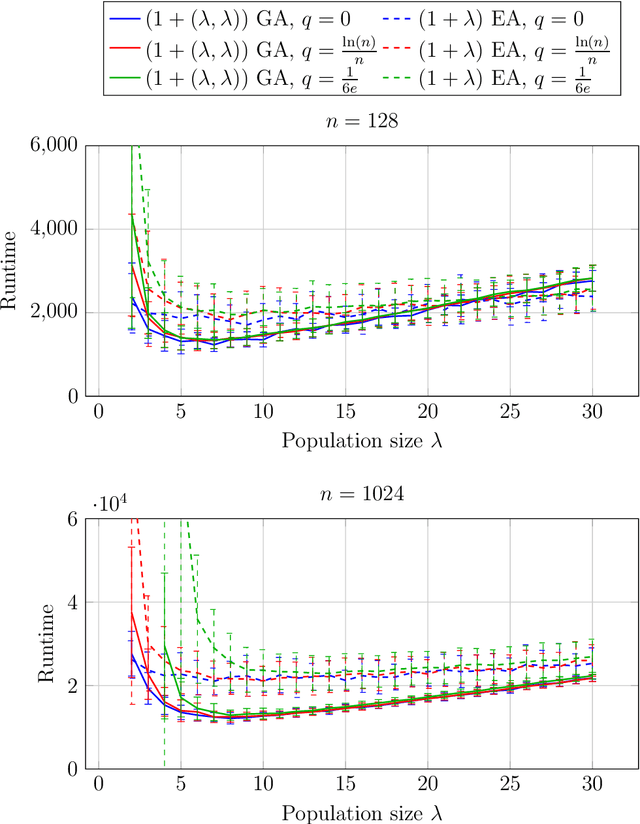
Evolutionary algorithms are known to be robust to noise in the evaluation of the fitness. In particular, larger offspring population sizes often lead to strong robustness. We analyze to what extent the $(1+(\lambda,\lambda))$ genetic algorithm is robust to noise. This algorithm also works with larger offspring population sizes, but an intermediate selection step and a non-standard use of crossover as repair mechanism could render this algorithm less robust than, e.g., the simple $(1+\lambda)$ evolutionary algorithm. Our experimental analysis on several classic benchmark problems shows that this difficulty does not arise. Surprisingly, in many situations this algorithm is even more robust to noise than the $(1+\lambda)$~EA.