Larger Offspring Populations Help the $(1 + (λ, λ))$ Genetic Algorithm to Overcome the Noise

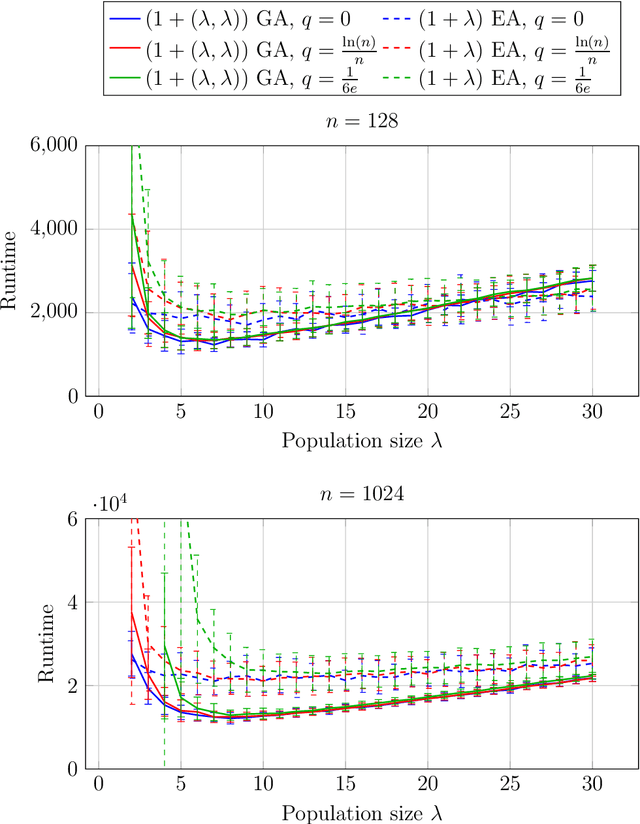
Evolutionary algorithms are known to be robust to noise in the evaluation of the fitness. In particular, larger offspring population sizes often lead to strong robustness. We analyze to what extent the $(1+(\lambda,\lambda))$ genetic algorithm is robust to noise. This algorithm also works with larger offspring population sizes, but an intermediate selection step and a non-standard use of crossover as repair mechanism could render this algorithm less robust than, e.g., the simple $(1+\lambda)$ evolutionary algorithm. Our experimental analysis on several classic benchmark problems shows that this difficulty does not arise. Surprisingly, in many situations this algorithm is even more robust to noise than the $(1+\lambda)$~EA.