Already Moderate Population Sizes Provably Yield Strong Robustness to Noise
Paper and Code
Apr 08, 2024
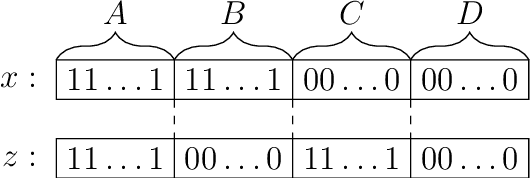
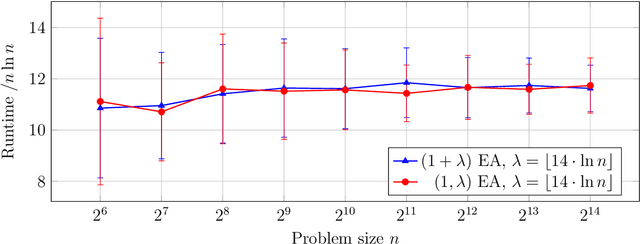
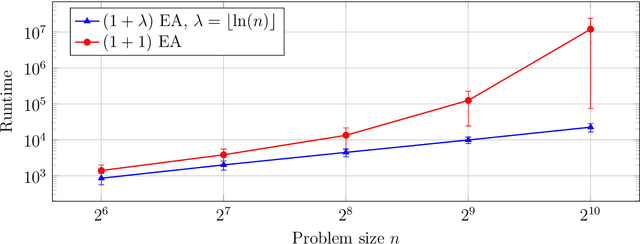
Experience shows that typical evolutionary algorithms can cope well with stochastic disturbances such as noisy function evaluations. In this first mathematical runtime analysis of the $(1+\lambda)$ and $(1,\lambda)$ evolutionary algorithms in the presence of prior bit-wise noise, we show that both algorithms can tolerate constant noise probabilities without increasing the asymptotic runtime on the OneMax benchmark. For this, a population size $\lambda$ suffices that is at least logarithmic in the problem size $n$. The only previous result in this direction regarded the less realistic one-bit noise model, required a population size super-linear in the problem size, and proved a runtime guarantee roughly cubic in the noiseless runtime for the OneMax benchmark. Our significantly stronger results are based on the novel proof argument that the noiseless offspring can be seen as a biased uniform crossover between the parent and the noisy offspring. We are optimistic that the technical lemmas resulting from this insight will find applications also in future mathematical runtime analyses of evolutionary algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge