CliniDigest: A Case Study in Large Language Model Based Large-Scale Summarization of Clinical Trial Descriptions

A clinical trial is a study that evaluates new biomedical interventions. To design new trials, researchers draw inspiration from those current and completed. In 2022, there were on average more than 100 clinical trials submitted to ClinicalTrials.gov every day, with each trial having a mean of approximately 1500 words [1]. This makes it nearly impossible to keep up to date. To mitigate this issue, we have created a batch clinical trial summarizer called CliniDigest using GPT-3.5. CliniDigest is, to our knowledge, the first tool able to provide real-time, truthful, and comprehensive summaries of clinical trials. CliniDigest can reduce up to 85 clinical trial descriptions (approximately 10,500 words) into a concise 200-word summary with references and limited hallucinations. We have tested CliniDigest on its ability to summarize 457 trials divided across 27 medical subdomains. For each field, CliniDigest generates summaries of $\mu=153,\ \sigma=69 $ words, each of which utilizes $\mu=54\%,\ \sigma=30\% $ of the sources. A more comprehensive evaluation is planned and outlined in this paper.

Neural Arithmetic Units

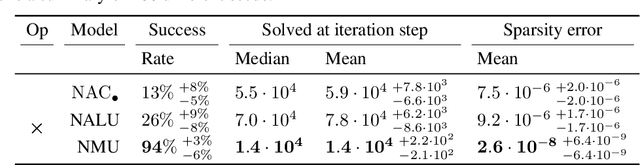
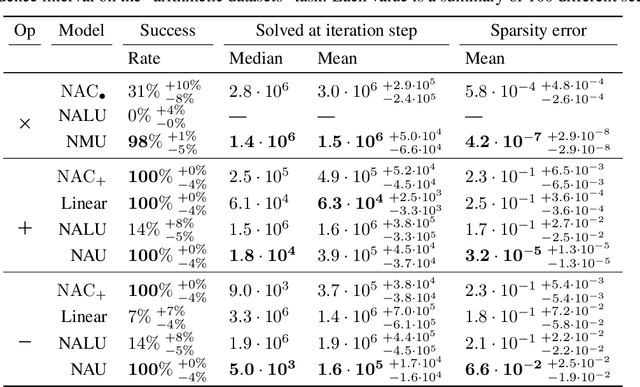
Neural networks can approximate complex functions, but they struggle to perform exact arithmetic operations over real numbers. The lack of inductive bias for arithmetic operations leaves neural networks without the underlying logic necessary to extrapolate on tasks such as addition, subtraction, and multiplication. We present two new neural network components: the Neural Addition Unit (NAU), which can learn exact addition and subtraction; and the Neural Multiplication Unit (NMU) that can multiply subsets of a vector. The NMU is, to our knowledge, the first arithmetic neural network component that can learn to multiply elements from a vector, when the hidden size is large. The two new components draw inspiration from a theoretical analysis of recently proposed arithmetic components. We find that careful initialization, restricting parameter space, and regularizing for sparsity is important when optimizing the NAU and NMU. Our proposed units NAU and NMU, compared with previous neural units, converge more consistently, have fewer parameters, learn faster, can converge for larger hidden sizes, obtain sparse and meaningful weights, and can extrapolate to negative and small values.

Autoencoding undirected molecular graphs with neural networks

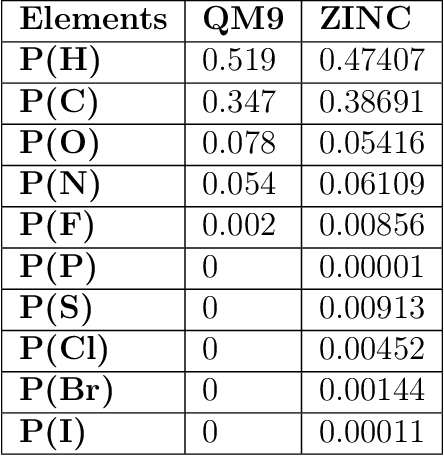
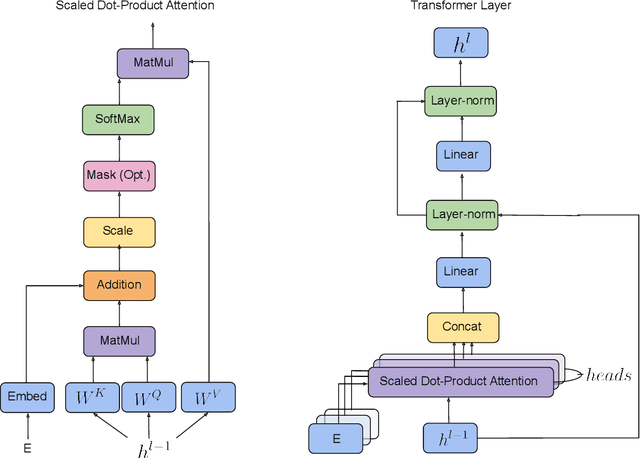
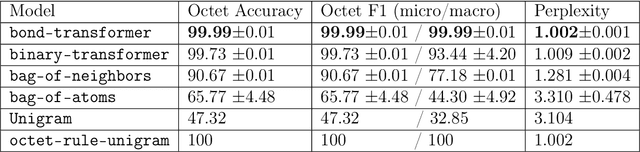
We propose a machine learning model, inspired by language modeling from natural language processing, which can automatically correct molecules in discrete representations using a structure rule learned from a collection of undirected molecular graphs. Using discrete representations of molecules allows cheap, fast, and coarse grained insights. We introduce an adaption on a modern neural network architecture, the Transformer, which can learn relationships between atoms and bonds. The algorithm thereby solves the unsupervised task of recovering partially observed molecules represented as undirected graphs. This is to our knowledge, the first work that can automatically learn any discrete molecular structure rule with input exclusively consisting of a training set of molecules. In this work the neural network successfully approximates the octet rule, relations in hypervalent molecules and ions when trained on the ZINC and QM9 dataset. These results provides encouraging evidence that neural networks can learn advanced molecular structure rules and dataset specific properties, as the transformer surpasses a strong octet-rule baseline.

Measuring Arithmetic Extrapolation Performance

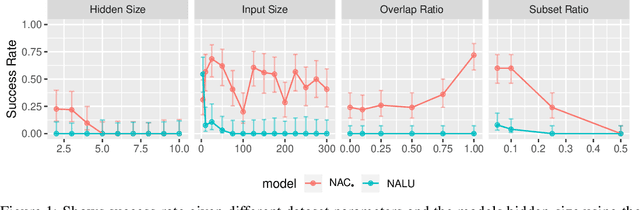
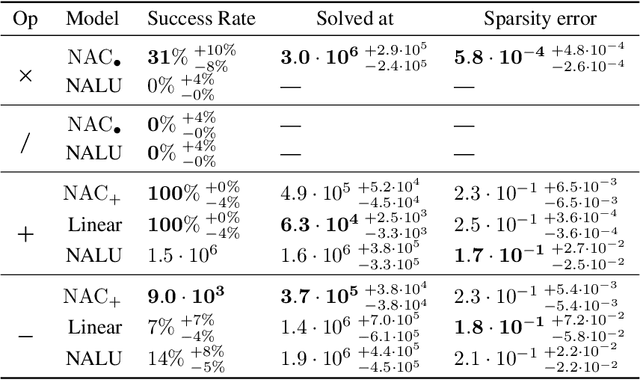
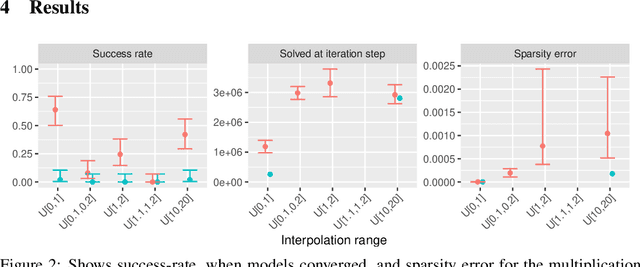
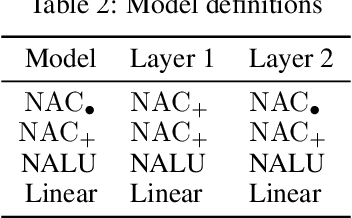
The Neural Arithmetic Logic Unit (NALU) is a neural network layer that can learn exact arithmetic operations between the elements of a hidden state. The goal of NALU is to learn perfect extrapolation, which requires learning the exact underlying logic of an unknown arithmetic problem. Evaluating the performance of the NALU is non-trivial as one arithmetic problem might have many solutions. As a consequence, single-instance MSE has been used to evaluate and compare performance between models. However, it can be hard to interpret what magnitude of MSE represents a correct solution and models sensitivity to initialization. We propose using a success-criterion to measure if and when a model converges. Using a success-criterion we can summarize success-rate over many initialization seeds and calculate confidence intervals. We contribute a generalized version of the previous arithmetic benchmark to measure models sensitivity under different conditions. This is, to our knowledge, the first extensive evaluation with respect to convergence of the NALU and its sub-units. Using a success-criterion to summarize 4800 experiments we find that consistently learning arithmetic extrapolation is challenging, in particular for multiplication.

Learning when to skim and when to read

Many recent advances in deep learning for natural language processing have come at increasing computational cost, but the power of these state-of-the-art models is not needed for every example in a dataset. We demonstrate two approaches to reducing unnecessary computation in cases where a fast but weak baseline classier and a stronger, slower model are both available. Applying an AUC-based metric to the task of sentiment classification, we find significant efficiency gains with both a probability-threshold method for reducing computational cost and one that uses a secondary decision network.

Neural Machine Translation with Characters and Hierarchical Encoding

Most existing Neural Machine Translation models use groups of characters or whole words as their unit of input and output. We propose a model with a hierarchical char2word encoder, that takes individual characters both as input and output. We first argue that this hierarchical representation of the character encoder reduces computational complexity, and show that it improves translation performance. Secondly, by qualitatively studying attention plots from the decoder we find that the model learns to compress common words into a single embedding whereas rare words, such as names and places, are represented character by character.