Atlas H&E-TME: Scalable AI-Based Tissue Profiling at Expert Pathologist-Level Accuracy

Hematoxylin and eosin (H&E) staining is the cornerstone of histopathology, yet scalable, quantitative analysis of H&E whole-slide images (WSIs) remains a central challenge in computational pathology. We present Atlas H&E-TME, an AI-based system built on the Atlas family of pathology foundation models that predicts tissue quality, tissue region, and cell type labels across multiple cancer types, yielding over 4,500 quantitative readouts per slide at cell-level resolution. A key challenge to validating such systems is overcoming morphological ambiguity inherent to H&E-only ground truth and the limited scalability of more informed references drawing on modalities such as immunohistochemistry (IHC). We address this with a dual validation framework combining biologically grounded depth with technical and morphological breadth. For depth, we propose an IHC-informed multi-pathologist consensus protocol that substantially improves inter-rater agreement over conventional H&E-only annotation. This yields a molecularly grounded reference against which we compare Atlas H&E-TME and pathologists working from H&E alone. For breadth, we benchmark Atlas H&E-TME on over 200,000 high-confidence H&E-only pathologist annotations across 1,500+ cases spanning eight cancer types and their most common metastatic sites, with subtypes covering >90% of clinical cases per cancer type, drawn from 25+ sources and 8+ scanner models. Benchmarked against the IHC-informed consensus, Atlas H&E-TME matches or exceeds pathologist H&E-only performance and generalizes consistently and robustly across this broad morphological and technical scope. In doing so, Atlas H&E-TME turns the H&E slide -- the most ubiquitous data in pathology -- into a scalable, quantitative window into the tumor and its microenvironment, laying a foundation for the next generation of tissue-based biomarkers in translational and clinical research.

In-Context Multiple Instance Learning

Multiple Instance Learning (MIL) addresses problems where supervision is available at the level of bags of instances and has been successfully applied in fields ranging from computational pathology to satellite imagery. Nevertheless, existing algorithms struggle in the low-label regime that characterizes many real-world applications. Flexible models overfit and rigid ones fail to adapt to the task at hand. We show that pretraining an in-context learner with a Perceiver-style architecture on synthetic data yields a model that can solve new tasks from a handful of labeled bags. At inference time, classification happens in a single forward pass and requires no gradient updates. We propose and investigate different synthetic data generators for bag-structured data and find that they capture complementary inductive biases. A model pretrained on a mixture of these generators inherits their per-task strengths and achieves the best average performance across twelve MIL benchmarks, outperforming supervised baselines that require task-specific training.

Mind the Gap: Continuous Magnification Sampling for Pathology Foundation Models

In histopathology, pathologists examine both tissue architecture at low magnification and fine-grained morphology at high magnification. Yet, the performance of pathology foundation models across magnifications and the effect of magnification sampling during training remain poorly understood. We model magnification sampling as a multi-source domain adaptation problem and develop a simple theoretical framework that reveals systematic trade-offs between sampling strategies. We show that the widely used discrete uniform sampling of magnifications (0.25, 0.5, 1.0, 2.0 mpp) leads to degradation at intermediate magnifications. We introduce continuous magnification sampling, which removes gaps in magnification coverage while preserving performance at standard scales. Further, we derive sampling distributions that optimize representation quality across magnification scales. To evaluate these strategies, we introduce two new benchmarks (TCGA-MS, BRACS-MS) with appropriate metrics. Our experiments show that continuous sampling substantially improves over discrete sampling at intermediate magnifications, with gains of up to 4 percentage points in balanced classification accuracy, and that optimized distributions can further improve performance. Finally, we evaluate current histopathology foundation models, finding that magnification is a primary driver of performance variation across models. Our work paves the way towards future pathology foundation models that perform reliably across magnifications.

Atlas: A Novel Pathology Foundation Model by Mayo Clinic, Charité, and Aignostics

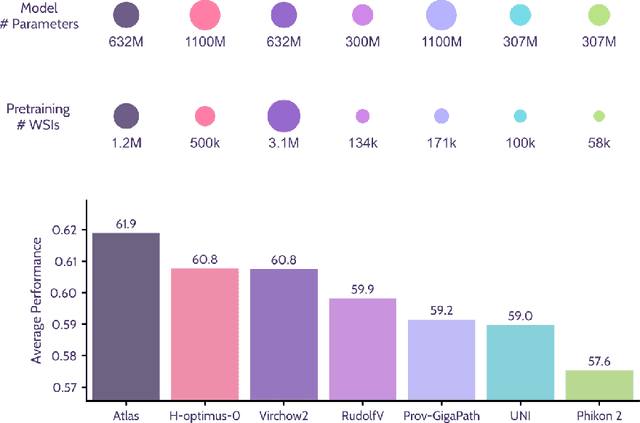
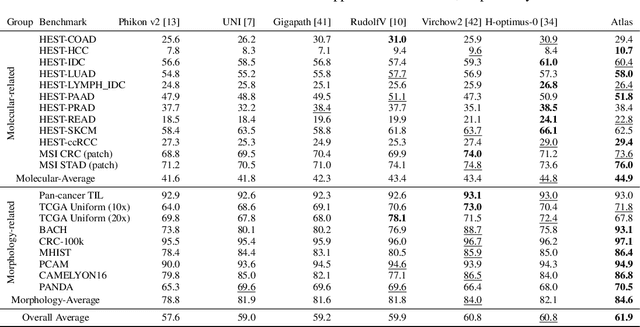
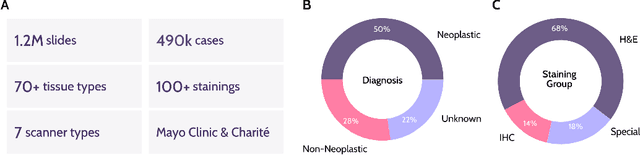
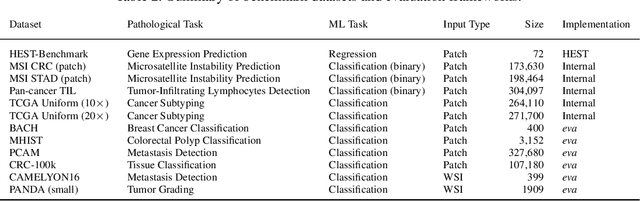
Recent advances in digital pathology have demonstrated the effectiveness of foundation models across diverse applications. In this report, we present Atlas, a novel vision foundation model based on the RudolfV approach. Our model was trained on a dataset comprising 1.2 million histopathology whole slide images, collected from two medical institutions: Mayo Clinic and Charit\'e - Universt\"atsmedizin Berlin. Comprehensive evaluations show that Atlas achieves state-of-the-art performance across twenty-one public benchmark datasets, even though it is neither the largest model by parameter count nor by training dataset size.

Uncertainty in Graph Contrastive Learning with Bayesian Neural Networks

Graph contrastive learning has shown great promise when labeled data is scarce, but large unlabeled datasets are available. However, it often does not take uncertainty estimation into account. We show that a variational Bayesian neural network approach can be used to improve not only the uncertainty estimates but also the downstream performance on semi-supervised node-classification tasks. Moreover, we propose a new measure of uncertainty for contrastive learning, that is based on the disagreement in likelihood due to different positive samples.

Hodge-Aware Contrastive Learning

Simplicial complexes prove effective in modeling data with multiway dependencies, such as data defined along the edges of networks or within other higher-order structures. Their spectrum can be decomposed into three interpretable subspaces via the Hodge decomposition, resulting foundational in numerous applications. We leverage this decomposition to develop a contrastive self-supervised learning approach for processing simplicial data and generating embeddings that encapsulate specific spectral information.Specifically, we encode the pertinent data invariances through simplicial neural networks and devise augmentations that yield positive contrastive examples with suitable spectral properties for downstream tasks. Additionally, we reweight the significance of negative examples in the contrastive loss, considering the similarity of their Hodge components to the anchor. By encouraging a stronger separation among less similar instances, we obtain an embedding space that reflects the spectral properties of the data. The numerical results on two standard edge flow classification tasks show a superior performance even when compared to supervised learning techniques. Our findings underscore the importance of adopting a spectral perspective for contrastive learning with higher-order data.