A mechanistically interpretable neural network for regulatory genomics

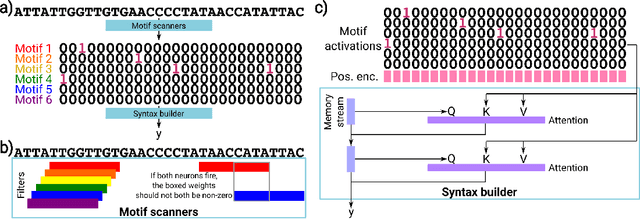
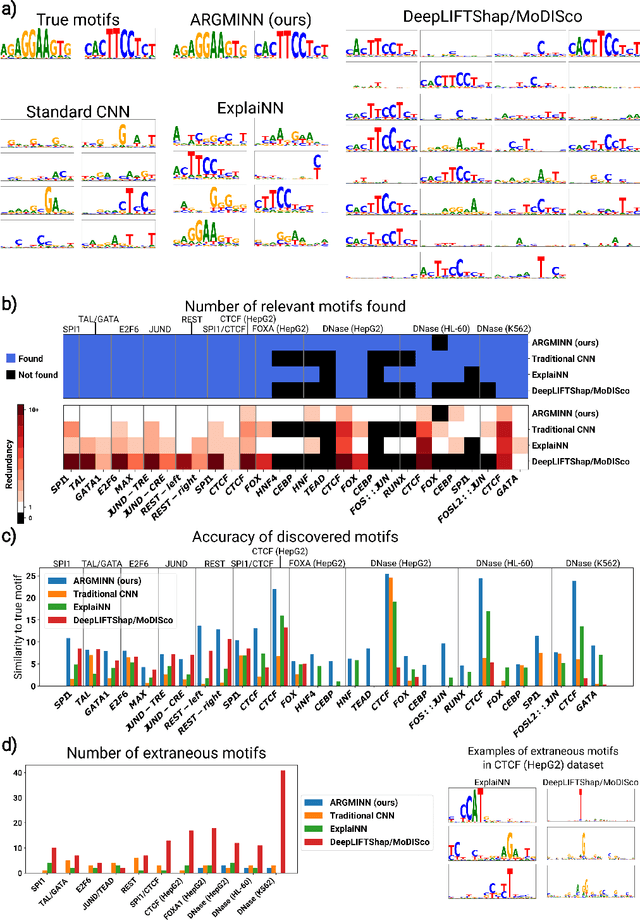
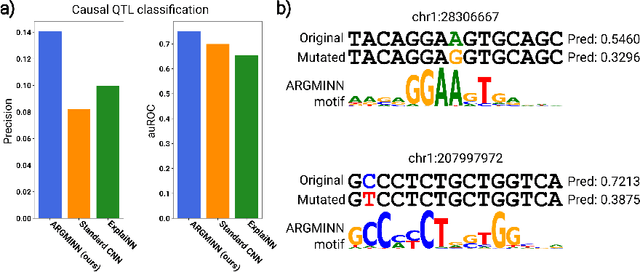
Deep neural networks excel in mapping genomic DNA sequences to associated readouts (e.g., protein-DNA binding). Beyond prediction, the goal of these networks is to reveal to scientists the underlying motifs (and their syntax) which drive genome regulation. Traditional methods that extract motifs from convolutional filters suffer from the uninterpretable dispersion of information across filters and layers. Other methods which rely on importance scores can be unstable and unreliable. Instead, we designed a novel mechanistically interpretable architecture for regulatory genomics, where motifs and their syntax are directly encoded and readable from the learned weights and activations. We provide theoretical and empirical evidence of our architecture's full expressivity, while still being highly interpretable. Through several experiments, we show that our architecture excels in de novo motif discovery and motif instance calling, is robust to variable sequence contexts, and enables fully interpretable generation of novel functional sequences.

Complex Preferences for Different Convergent Priors in Discrete Graph Diffusion

Diffusion models have achieved state-of-the-art performance in generating many different kinds of data, including images, text, and videos. Despite their success, there has been limited research on how the underlying diffusion process and the final convergent prior can affect generative performance; this research has also been limited to continuous data types and a score-based diffusion framework. To fill this gap, we explore how different discrete diffusion kernels (which converge to different prior distributions) affect the performance of diffusion models for graphs. To this end, we developed a novel formulation of a family of discrete diffusion kernels which are easily adjustable to converge to different Bernoulli priors, and we study the effect of these different kernels on generative performance. We show that the quality of generated graphs is sensitive to the prior used, and that the optimal choice cannot be explained by obvious statistics or metrics, which challenges the intuitions which previous works have suggested.

RINGER: Rapid Conformer Generation for Macrocycles with Sequence-Conditioned Internal Coordinate Diffusion

Macrocyclic peptides are an emerging therapeutic modality, yet computational approaches for accurately sampling their diverse 3D ensembles remain challenging due to their conformational diversity and geometric constraints. Here, we introduce RINGER, a diffusion-based transformer model for sequence-conditioned generation of macrocycle structures based on internal coordinates. RINGER provides fast backbone sampling while respecting key structural invariances of cyclic peptides. Through extensive benchmarking and analysis against gold-standard conformer ensembles of cyclic peptides generated with metadynamics, we demonstrate how RINGER generates both high-quality and diverse geometries at a fraction of the computational cost. Our work lays the foundation for improved sampling of cyclic geometries and the development of geometric learning methods for peptides.

GraphGUIDE: interpretable and controllable conditional graph generation with discrete Bernoulli diffusion

Diffusion models achieve state-of-the-art performance in generating realistic objects and have been successfully applied to images, text, and videos. Recent work has shown that diffusion can also be defined on graphs, including graph representations of drug-like molecules. Unfortunately, it remains difficult to perform conditional generation on graphs in a way which is interpretable and controllable. In this work, we propose GraphGUIDE, a novel framework for graph generation using diffusion models, where edges in the graph are flipped or set at each discrete time step. We demonstrate GraphGUIDE on several graph datasets, and show that it enables full control over the conditional generation of arbitrary structural properties without relying on predefined labels. Our framework for graph diffusion can have a large impact on the interpretable conditional generation of graphs, including the generation of drug-like molecules with desired properties in a way which is informed by experimental evidence.

Improving Graph Generation by Restricting Graph Bandwidth

Deep graph generative modeling has proven capable of learning the distribution of complex, multi-scale structures characterizing real-world graphs. However, one of the main limitations of existing methods is their large output space, which limits generation scalability and hinders accurate modeling of the underlying distribution. To overcome these limitations, we propose a novel approach that significantly reduces the output space of existing graph generative models. Specifically, starting from the observation that many real-world graphs have low graph bandwidth, we restrict graph bandwidth during training and generation. Our strategy improves both generation scalability and quality without increasing architectural complexity or reducing expressiveness. Our approach is compatible with existing graph generative methods, and we describe its application to both autoregressive and one-shot models. We extensively validate our strategy on synthetic and real datasets, including molecular graphs. Our experiments show that, in addition to improving generation efficiency, our approach consistently improves generation quality and reconstruction accuracy. The implementation is made available.

Hierarchically branched diffusion models for efficient and interpretable multi-class conditional generation

Diffusion models have achieved justifiable popularity by attaining state-of-the-art performance in generating realistic objects from seemingly arbitrarily complex data distributions, including when conditioning generation on labels. Unfortunately, however, their iterative nature renders them very computationally inefficient during the sampling process. For the multi-class conditional generation problem, we propose a novel, structurally unique framework of diffusion models which are hierarchically branched according to the inherent relationships between classes. In this work, we demonstrate that branched diffusion models offer major improvements in efficiently generating samples from multiple classes. We also showcase several other advantages of branched diffusion models, including ease of extension to novel classes in a continual-learning setting, and a unique interpretability that offers insight into these generative models. Branched diffusion models represent an alternative paradigm to their traditional linear counterparts, and can have large impacts in how we use diffusion models for efficient generation, online learning, and scientific discovery.