Sequential Predictive Two-Sample and Independence Testing

We study the problems of sequential nonparametric two-sample and independence testing. Sequential tests process data online and allow using observed data to decide whether to stop and reject the null hypothesis or to collect more data while maintaining type I error control. We build upon the principle of (nonparametric) testing by betting, where a gambler places bets on future observations and their wealth measures evidence against the null hypothesis. While recently developed kernel-based betting strategies often work well on simple distributions, selecting a suitable kernel for high-dimensional or structured data, such as text and images, is often nontrivial. To address this drawback, we design prediction-based betting strategies that rely on the following fact: if a sequentially updated predictor starts to consistently determine (a) which distribution an instance is drawn from, or (b) whether an instance is drawn from the joint distribution or the product of the marginal distributions (the latter produced by external randomization), it provides evidence against the two-sample or independence nulls respectively. We empirically demonstrate the superiority of our tests over kernel-based approaches under structured settings. Our tests can be applied beyond the case of independent and identically distributed data, remaining valid and powerful even when the data distribution drifts over time.

Sequential Kernelized Independence Testing

Independence testing is a fundamental and classical statistical problem that has been extensively studied in the batch setting when one fixes the sample size before collecting data. However, practitioners often prefer procedures that adapt to the complexity of a problem at hand instead of setting sample size in advance. Ideally, such procedures should (a) allow stopping earlier on easy tasks (and later on harder tasks), hence making better use of available resources, and (b) continuously monitor the data and efficiently incorporate statistical evidence after collecting new data, while controlling the false alarm rate. It is well known that classical batch tests are not tailored for streaming data settings, since valid inference after data peeking requires correcting for multiple testing, but such corrections generally result in low power. In this paper, we design sequential kernelized independence tests (SKITs) that overcome such shortcomings based on the principle of testing by betting. We exemplify our broad framework using bets inspired by kernelized dependence measures such as the Hilbert-Schmidt independence criterion (HSIC) and the constrained-covariance criterion (COCO). Importantly, we also generalize the framework to non-i.i.d. time-varying settings, for which there exist no batch tests. We demonstrate the power of our approaches on both simulated and real data.

Tracking the risk of a deployed model and detecting harmful distribution shifts

When deployed in the real world, machine learning models inevitably encounter changes in the data distribution, and certain -- but not all -- distribution shifts could result in significant performance degradation. In practice, it may make sense to ignore benign shifts, under which the performance of a deployed model does not degrade substantially, making interventions by a human expert (or model retraining) unnecessary. While several works have developed tests for distribution shifts, these typically either use non-sequential methods, or detect arbitrary shifts (benign or harmful), or both. We argue that a sensible method for firing off a warning has to both (a) detect harmful shifts while ignoring benign ones, and (b) allow continuous monitoring of model performance without increasing the false alarm rate. In this work, we design simple sequential tools for testing if the difference between source (training) and target (test) distributions leads to a significant drop in a risk function of interest, like accuracy or calibration. Recent advances in constructing time-uniform confidence sequences allow efficient aggregation of statistical evidence accumulated during the tracking process. The designed framework is applicable in settings where (some) true labels are revealed after the prediction is performed, or when batches of labels become available in a delayed fashion. We demonstrate the efficacy of the proposed framework through an extensive empirical study on a collection of simulated and real datasets.

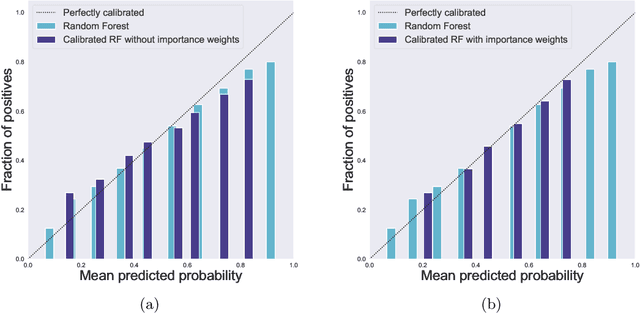
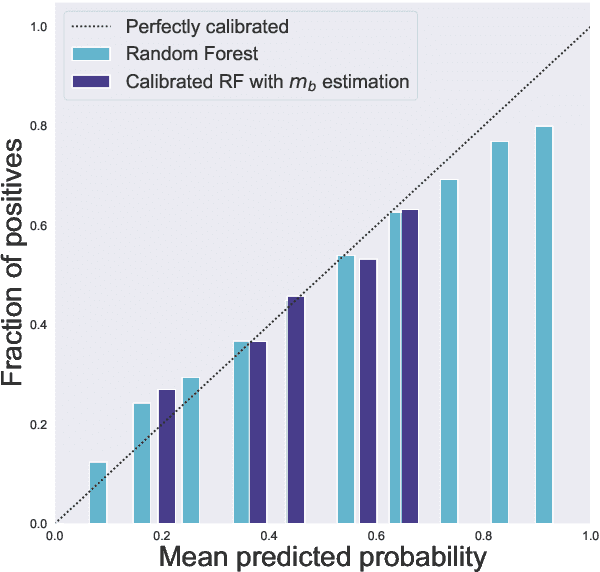
Distribution-free uncertainty quantification for classification under label shift

Trustworthy deployment of ML models requires a proper measure of uncertainty, especially in safety-critical applications. We focus on uncertainty quantification (UQ) for classification problems via two avenues -- prediction sets using conformal prediction and calibration of probabilistic predictors by post-hoc binning -- since these possess distribution-free guarantees for i.i.d. data. Two common ways of generalizing beyond the i.i.d. setting include handling covariate and label shift. Within the context of distribution-free UQ, the former has already received attention, but not the latter. It is known that label shift hurts prediction, and we first argue that it also hurts UQ, by showing degradation in coverage and calibration. Piggybacking on recent progress in addressing label shift (for better prediction), we examine the right way to achieve UQ by reweighting the aforementioned conformal and calibration procedures whenever some unlabeled data from the target distribution is available. We examine these techniques theoretically in a distribution-free framework and demonstrate their excellent practical performance.

Distribution-free binary classification: prediction sets, confidence intervals and calibration

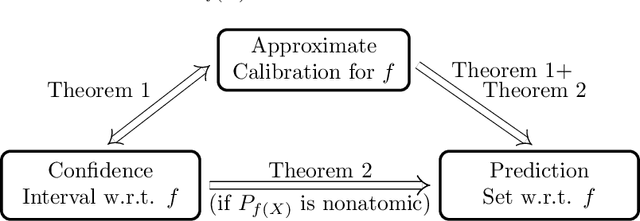
We study three notions of uncertainty quantification---calibration, confidence intervals and prediction sets---for binary classification in the distribution-free setting, that is without making any distributional assumptions on the data. With a focus towards calibration, we establish a 'tripod' of theorems that connect these three notions for score-based classifiers. A direct implication is that distribution-free calibration is only possible, even asymptotically, using a scoring function whose level sets partition the feature space into at most countably many sets. Parametric calibration schemes such as variants of Platt scaling do not satisfy this requirement, while nonparametric schemes based on binning do. To close the loop, we derive distribution-free confidence intervals for binned probabilities for both fixed-width and uniform-mass binning. As a consequence of our 'tripod' theorems, these confidence intervals for binned probabilities lead to distribution-free calibration. We also derive extensions to settings with streaming data and covariate shift.