Building symmetries into data-driven manifold dynamics models for complex flows

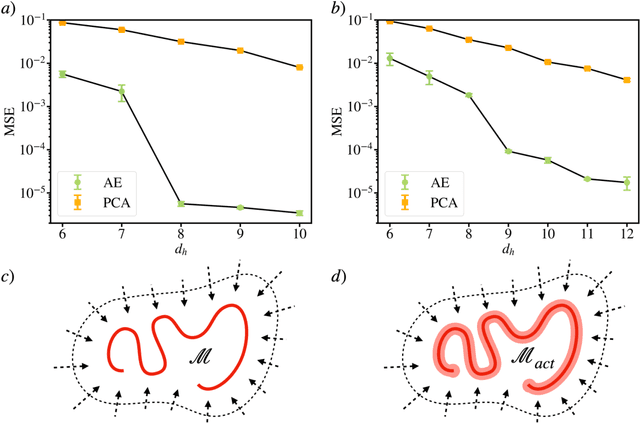
Symmetries in a dynamical system provide an opportunity to dramatically improve the performance of data-driven models. For fluid flows, such models are needed for tasks related to design, understanding, prediction, and control. In this work we exploit the symmetries of the Navier-Stokes equations (NSE) and use simulation data to find the manifold where the long-time dynamics live, which has many fewer degrees of freedom than the full state representation, and the evolution equation for the dynamics on that manifold. We call this method ''symmetry charting''. The first step is to map to a ''fundamental chart'', which is a region in the state space of the flow to which all other regions can be mapped by a symmetry operation. To map to the fundamental chart we identify a set of indicators from the Fourier transform that uniquely identify the symmetries of the system. We then find a low-dimensional coordinate representation of the data in the fundamental chart with the use of an autoencoder. We use a variation called an implicit rank minimizing autoencoder with weight decay, which in addition to compressing the dimension of the data, also gives estimates of how many dimensions are needed to represent the data: i.e. the dimension of the invariant manifold of the long-time dynamics. Finally, we learn dynamics on this manifold with the use of neural ordinary differential equations. We apply symmetry charting to two-dimensional Kolmogorov flow in a chaotic bursting regime. This system has a continuous translation symmetry, and discrete rotation and shift-reflect symmetries. With this framework we observe that less data is needed to learn accurate data-driven models, more robust estimates of the manifold dimension are obtained, equivariance of the NSE is satisfied, better short-time tracking with respect to the true data is observed, and long-time statistics are correctly captured.

Enhancing Predictive Capabilities in Data-Driven Dynamical Modeling with Automatic Differentiation: Koopman and Neural ODE Approaches

Data-driven approximations of the Koopman operator are promising for predicting the time evolution of systems characterized by complex dynamics. Among these methods, the approach known as extended dynamic mode decomposition with dictionary learning (EDMD-DL) has garnered significant attention. Here we present a modification of EDMD-DL that concurrently determines both the dictionary of observables and the corresponding approximation of the Koopman operator. This innovation leverages automatic differentiation to facilitate gradient descent computations through the pseudoinverse. We also address the performance of several alternative methodologies. We assess a 'pure' Koopman approach, which involves the direct time-integration of a linear, high-dimensional system governing the dynamics within the space of observables. Additionally, we explore a modified approach where the system alternates between spaces of states and observables at each time step -- this approach no longer satisfies the linearity of the true Koopman operator representation. For further comparisons, we also apply a state space approach (neural ODEs). We consider systems encompassing two and three-dimensional ordinary differential equation systems featuring steady, oscillatory, and chaotic attractors, as well as partial differential equations exhibiting increasingly complex and intricate behaviors. Our framework significantly outperforms EDMD-DL. Furthermore, the state space approach offers superior performance compared to the 'pure' Koopman approach where the entire time evolution occurs in the space of observables. When the temporal evolution of the Koopman approach alternates between states and observables at each time step, however, its predictions become comparable to those of the state space approach.

Turbulence control in plane Couette flow using low-dimensional neural ODE-based models and deep reinforcement learning

The high dimensionality and complex dynamics of turbulent flows remain an obstacle to the discovery and implementation of control strategies. Deep reinforcement learning (RL) is a promising avenue for overcoming these obstacles, but requires a training phase in which the RL agent iteratively interacts with the flow environment to learn a control policy, which can be prohibitively expensive when the environment involves slow experiments or large-scale simulations. We overcome this challenge using a framework we call "DManD-RL" (data-driven manifold dynamics-RL), which generates a data-driven low-dimensional model of our system that we use for RL training. With this approach, we seek to minimize drag in a direct numerical simulation (DNS) of a turbulent minimal flow unit of plane Couette flow at Re=400 using two slot jets on one wall. We obtain, from DNS data with $\mathcal{O}(10^5)$ degrees of freedom, a 25-dimensional DManD model of the dynamics by combining an autoencoder and neural ordinary differential equation. Using this model as the environment, we train an RL control agent, yielding a 440-fold speedup over training on the DNS, with equivalent control performance. The agent learns a policy that laminarizes 84% of unseen DNS test trajectories within 900 time units, significantly outperforming classical opposition control (58%), despite the actuation authority being much more restricted. The agent often achieves laminarization through a counterintuitive strategy that drives the formation of two low-speed streaks, with a spanwise wavelength that is too small to be self-sustaining. The agent demonstrates the same performance when we limit observations to wall shear rate.

Dynamics of a data-driven low-dimensional model of turbulent minimal Couette flow

Because the Navier-Stokes equations are dissipative, the long-time dynamics of a flow in state space are expected to collapse onto a manifold whose dimension may be much lower than the dimension required for a resolved simulation. On this manifold, the state of the system can be exactly described in a coordinate system parameterizing the manifold. Describing the system in this low-dimensional coordinate system allows for much faster simulations and analysis. We show, for turbulent Couette flow, that this description of the dynamics is possible using a data-driven manifold dynamics modeling method. This approach consists of an autoencoder to find a low-dimensional manifold coordinate system and a set of ordinary differential equations defined by a neural network. Specifically, we apply this method to minimal flow unit turbulent plane Couette flow at $\textit{Re}=400$, where a fully resolved solutions requires $\mathcal{O}(10^5)$ degrees of freedom. Using only data from this simulation we build models with fewer than $20$ degrees of freedom that quantitatively capture key characteristics of the flow, including the streak breakdown and regeneration cycle. At short-times, the models track the true trajectory for multiple Lyapunov times, and, at long-times, the models capture the Reynolds stress and the energy balance. For comparison, we show that the models outperform POD-Galerkin models with $\sim$2000 degrees of freedom. Finally, we compute unstable periodic orbits from the models. Many of these closely resemble previously computed orbits for the full system; additionally, we find nine orbits that correspond to previously unknown solutions in the full system.

Data-driven control of spatiotemporal chaos with reduced-order neural ODE-based models and reinforcement learning

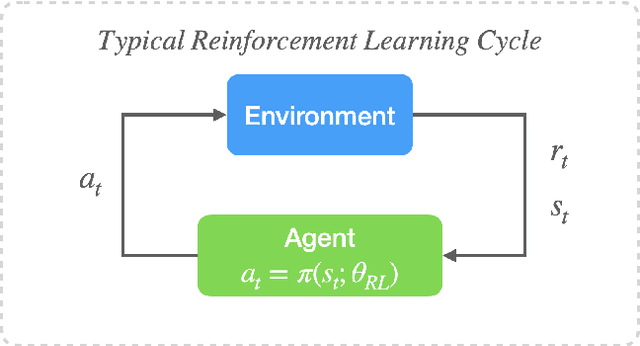
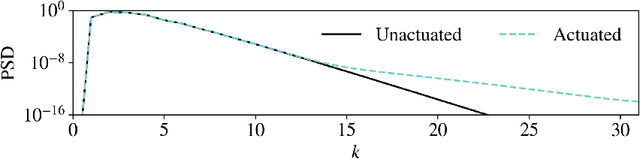
Deep reinforcement learning (RL) is a data-driven method capable of discovering complex control strategies for high-dimensional systems, making it promising for flow control applications. In particular, the present work is motivated by the goal of reducing energy dissipation in turbulent flows, and the example considered is the spatiotemporally chaotic dynamics of the Kuramoto-Sivashinsky equation (KSE). A major challenge associated with RL is that substantial training data must be generated by repeatedly interacting with the target system, making it costly when the system is computationally or experimentally expensive. We mitigate this challenge in a data-driven manner by combining dimensionality reduction via an autoencoder with a neural ODE framework to obtain a low-dimensional dynamical model from just a limited data set. We substitute this data-driven reduced-order model (ROM) in place of the true system during RL training to efficiently estimate the optimal policy, which can then be deployed on the true system. For the KSE actuated with localized forcing ("jets") at four locations, we demonstrate that we are able to learn a ROM that accurately captures the actuated dynamics as well as the underlying natural dynamics just from snapshots of the KSE experiencing random actuations. Using this ROM and a control objective of minimizing dissipation and power cost, we extract a control policy from it using deep RL. We show that the ROM-based control strategy translates well to the true KSE and highlight that the RL agent discovers and stabilizes an underlying forced equilibrium solution of the KSE system. We show that this forced equilibrium captured in the ROM and discovered through RL is related to an existing known equilibrium solution of the natural KSE.

Stabilized Neural Ordinary Differential Equations for Long-Time Forecasting of Dynamical Systems

In data-driven modeling of spatiotemporal phenomena careful consideration often needs to be made in capturing the dynamics of the high wavenumbers. This problem becomes especially challenging when the system of interest exhibits shocks or chaotic dynamics. We present a data-driven modeling method that accurately captures shocks and chaotic dynamics by proposing a novel architecture, stabilized neural ordinary differential equation (ODE). In our proposed architecture, we learn the right-hand-side (RHS) of an ODE by adding the outputs of two NN together where one learns a linear term and the other a nonlinear term. Specifically, we implement this by training a sparse linear convolutional NN to learn the linear term and a dense fully-connected nonlinear NN to learn the nonlinear term. This is in contrast with the standard neural ODE which involves training only a single NN for learning the RHS. We apply this setup to the viscous Burgers equation, which exhibits shocked behavior, and show better short-time tracking and prediction of the energy spectrum at high wavenumbers than a standard neural ODE. We also find that the stabilized neural ODE models are much more robust to noisy initial conditions than the standard neural ODE approach. We also apply this method to chaotic trajectories of the Kuramoto-Sivashinsky equation. In this case, stabilized neural ODEs keep long-time trajectories on the attractor, and are highly robust to noisy initial conditions, while standard neural ODEs fail at achieving either of these results. We conclude by demonstrating how stabilizing neural ODEs provide a natural extension for use in reduced-order modeling by projecting the dynamics onto the eigenvectors of the learned linear term.

Data-Driven Reduced-Order Modeling of Spatiotemporal Chaos with Neural Ordinary Differential Equations

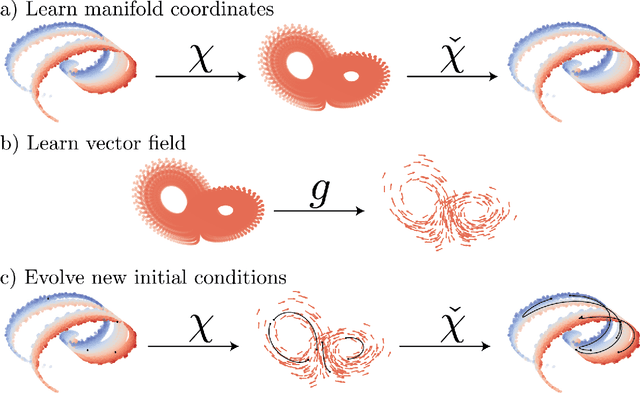
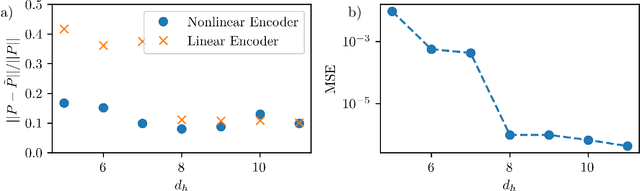
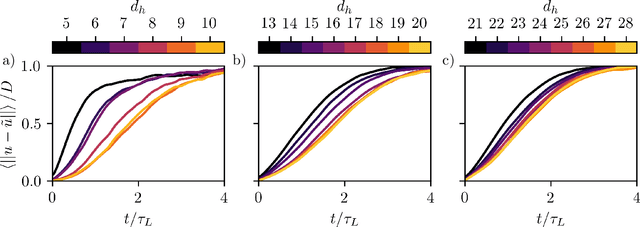
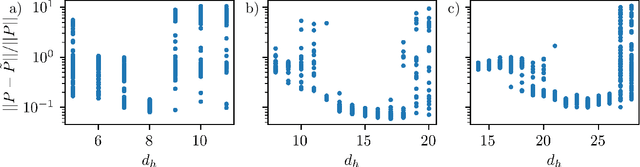
Dissipative partial differential equations that exhibit chaotic dynamics tend to evolve to attractors that exist on finite-dimensional manifolds. We present a data-driven reduced order modeling method that capitalizes on this fact by finding the coordinates of this manifold and finding an ordinary differential equation (ODE) describing the dynamics in this coordinate system. The manifold coordinates are discovered using an undercomplete autoencoder -- a neural network (NN) that reduces then expands dimension. Then the ODE, in these coordinates, is approximated by a NN using the neural ODE framework. Both of these methods only require snapshots of data to learn a model, and the data can be widely and/or unevenly spaced. We apply this framework to the Kuramoto-Sivashinsky for different domain sizes that exhibit chaotic dynamics. With this system, we find that dimension reduction improves performance relative to predictions in the ambient space, where artifacts arise. Then, with the low-dimensional model, we vary the training data spacing and find excellent short- and long-time statistical recreation of the true dynamics for widely spaced data (spacing of ~0.7 Lyapunov times). We end by comparing performance with various degrees of dimension reduction, and find a "sweet spot" in terms of performance vs. dimension.

Deep learning to discover and predict dynamics on an inertial manifold

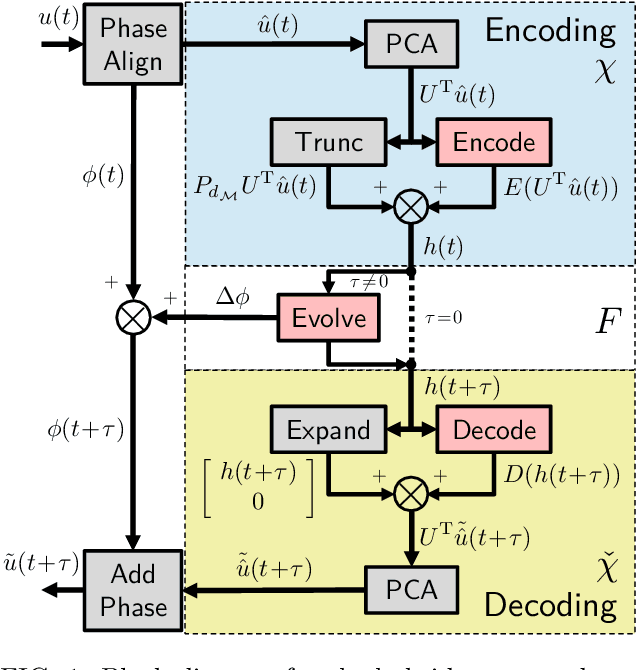
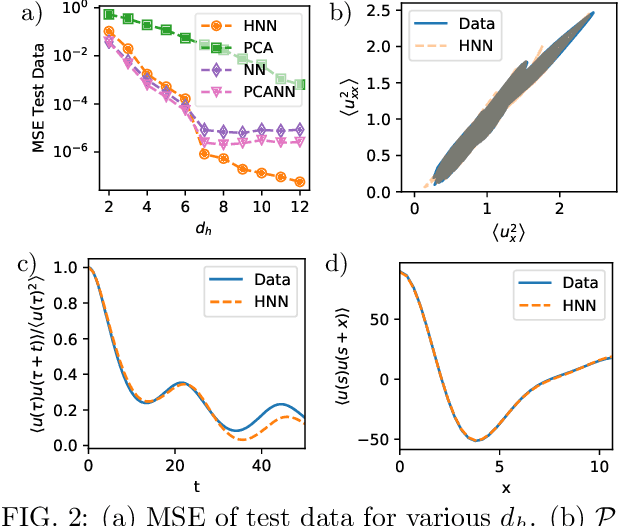
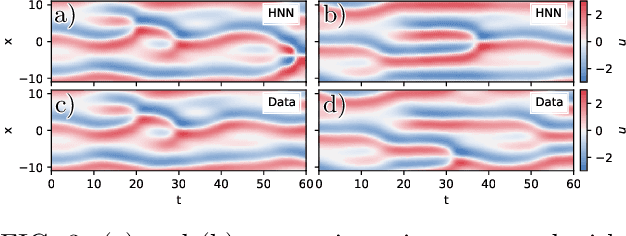
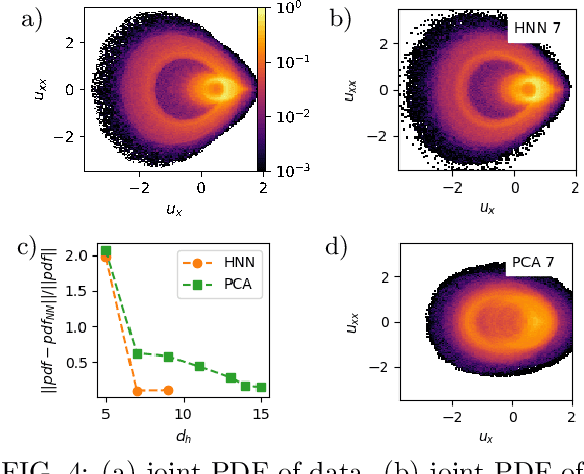
A data-driven framework is developed to represent chaotic dynamics on an inertial manifold (IM), and applied to solutions of the Kuramoto-Sivashinsky equation. A hybrid method combining linear and nonlinear (neural-network) dimension reduction transforms between coordinates in the full state space and on the IM. Additional neural networks predict time-evolution on the IM. The formalism accounts for translation invariance and energy conservation, and substantially outperforms linear dimension reduction, reproducing very well key dynamic and statistical features of the attractor.