Deep learning to discover and predict dynamics on an inertial manifold
Paper and Code
Dec 20, 2019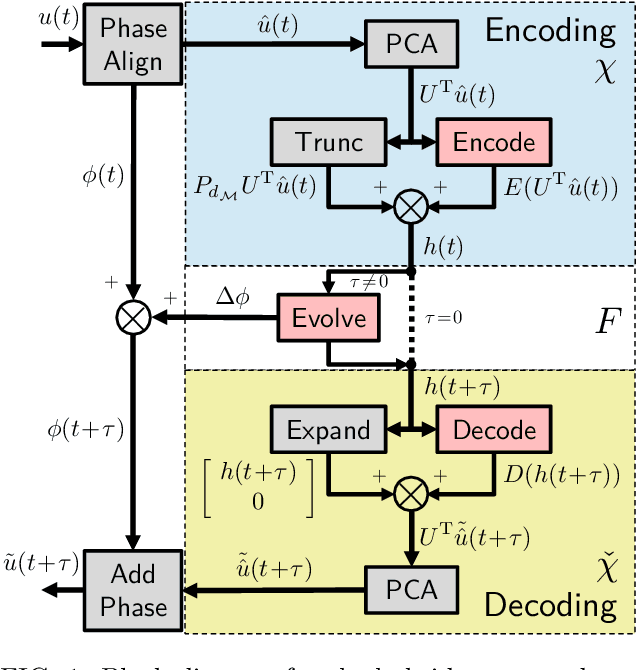
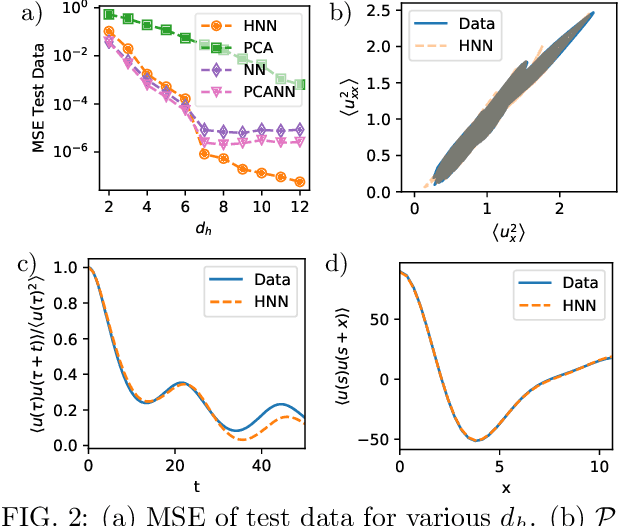
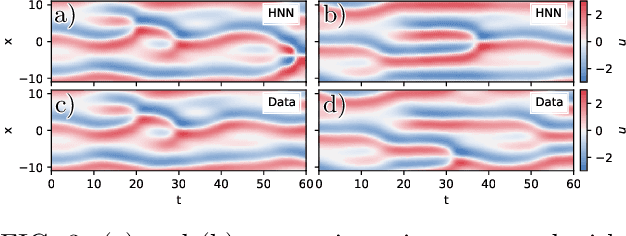
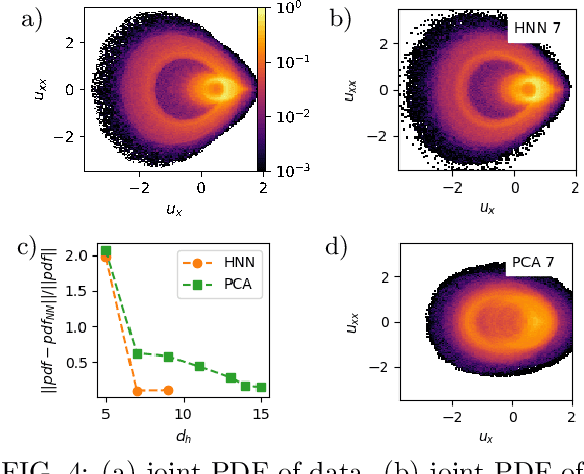
A data-driven framework is developed to represent chaotic dynamics on an inertial manifold (IM), and applied to solutions of the Kuramoto-Sivashinsky equation. A hybrid method combining linear and nonlinear (neural-network) dimension reduction transforms between coordinates in the full state space and on the IM. Additional neural networks predict time-evolution on the IM. The formalism accounts for translation invariance and energy conservation, and substantially outperforms linear dimension reduction, reproducing very well key dynamic and statistical features of the attractor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge