Autoencoders for discovering manifold dimension and coordinates in data from complex dynamical systems

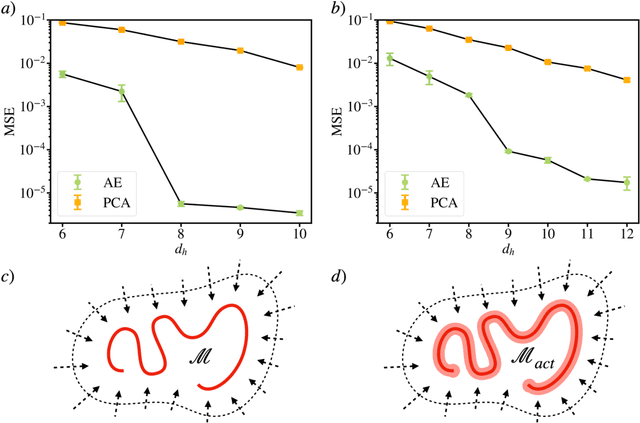
While many phenomena in physics and engineering are formally high-dimensional, their long-time dynamics often live on a lower-dimensional manifold. The present work introduces an autoencoder framework that combines implicit regularization with internal linear layers and $L_2$ regularization (weight decay) to automatically estimate the underlying dimensionality of a data set, produce an orthogonal manifold coordinate system, and provide the mapping functions between the ambient space and manifold space, allowing for out-of-sample projections. We validate our framework's ability to estimate the manifold dimension for a series of datasets from dynamical systems of varying complexities and compare to other state-of-the-art estimators. We analyze the training dynamics of the network to glean insight into the mechanism of low-rank learning and find that collectively each of the implicit regularizing layers compound the low-rank representation and even self-correct during training. Analysis of gradient descent dynamics for this architecture in the linear case reveals the role of the internal linear layers in leading to faster decay of a "collective weight variable" incorporating all layers, and the role of weight decay in breaking degeneracies and thus driving convergence along directions in which no decay would occur in its absence. We show that this framework can be naturally extended for applications of state-space modeling and forecasting by generating a data-driven dynamic model of a spatiotemporally chaotic partial differential equation using only the manifold coordinates. Finally, we demonstrate that our framework is robust to hyperparameter choices.

Turbulence control in plane Couette flow using low-dimensional neural ODE-based models and deep reinforcement learning

The high dimensionality and complex dynamics of turbulent flows remain an obstacle to the discovery and implementation of control strategies. Deep reinforcement learning (RL) is a promising avenue for overcoming these obstacles, but requires a training phase in which the RL agent iteratively interacts with the flow environment to learn a control policy, which can be prohibitively expensive when the environment involves slow experiments or large-scale simulations. We overcome this challenge using a framework we call "DManD-RL" (data-driven manifold dynamics-RL), which generates a data-driven low-dimensional model of our system that we use for RL training. With this approach, we seek to minimize drag in a direct numerical simulation (DNS) of a turbulent minimal flow unit of plane Couette flow at Re=400 using two slot jets on one wall. We obtain, from DNS data with $\mathcal{O}(10^5)$ degrees of freedom, a 25-dimensional DManD model of the dynamics by combining an autoencoder and neural ordinary differential equation. Using this model as the environment, we train an RL control agent, yielding a 440-fold speedup over training on the DNS, with equivalent control performance. The agent learns a policy that laminarizes 84% of unseen DNS test trajectories within 900 time units, significantly outperforming classical opposition control (58%), despite the actuation authority being much more restricted. The agent often achieves laminarization through a counterintuitive strategy that drives the formation of two low-speed streaks, with a spanwise wavelength that is too small to be self-sustaining. The agent demonstrates the same performance when we limit observations to wall shear rate.

Data-driven control of spatiotemporal chaos with reduced-order neural ODE-based models and reinforcement learning

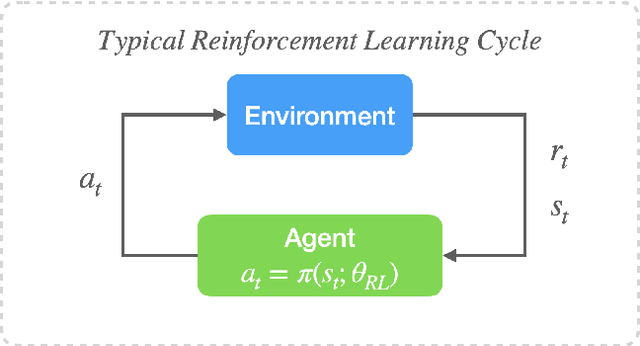
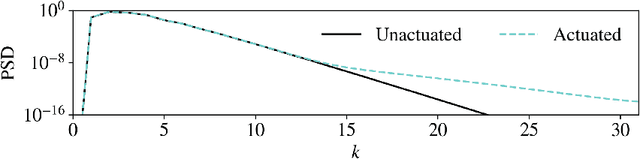
Deep reinforcement learning (RL) is a data-driven method capable of discovering complex control strategies for high-dimensional systems, making it promising for flow control applications. In particular, the present work is motivated by the goal of reducing energy dissipation in turbulent flows, and the example considered is the spatiotemporally chaotic dynamics of the Kuramoto-Sivashinsky equation (KSE). A major challenge associated with RL is that substantial training data must be generated by repeatedly interacting with the target system, making it costly when the system is computationally or experimentally expensive. We mitigate this challenge in a data-driven manner by combining dimensionality reduction via an autoencoder with a neural ODE framework to obtain a low-dimensional dynamical model from just a limited data set. We substitute this data-driven reduced-order model (ROM) in place of the true system during RL training to efficiently estimate the optimal policy, which can then be deployed on the true system. For the KSE actuated with localized forcing ("jets") at four locations, we demonstrate that we are able to learn a ROM that accurately captures the actuated dynamics as well as the underlying natural dynamics just from snapshots of the KSE experiencing random actuations. Using this ROM and a control objective of minimizing dissipation and power cost, we extract a control policy from it using deep RL. We show that the ROM-based control strategy translates well to the true KSE and highlight that the RL agent discovers and stabilizes an underlying forced equilibrium solution of the KSE system. We show that this forced equilibrium captured in the ROM and discovered through RL is related to an existing known equilibrium solution of the natural KSE.

Symmetry reduction for deep reinforcement learning active control of chaotic spatiotemporal dynamics

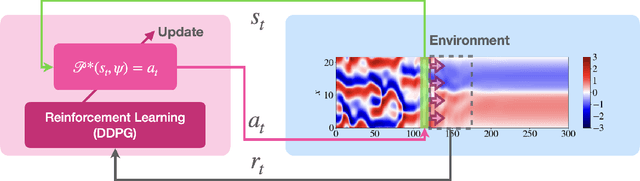
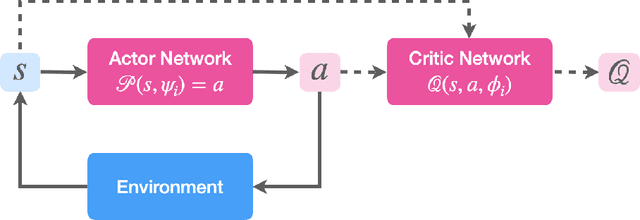
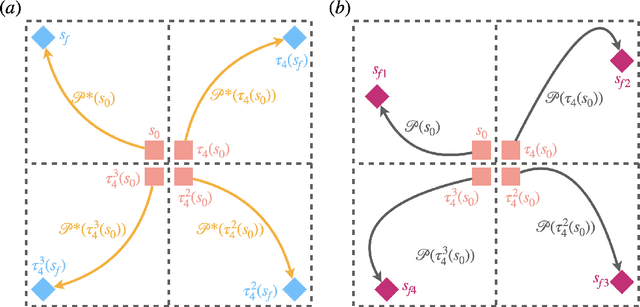
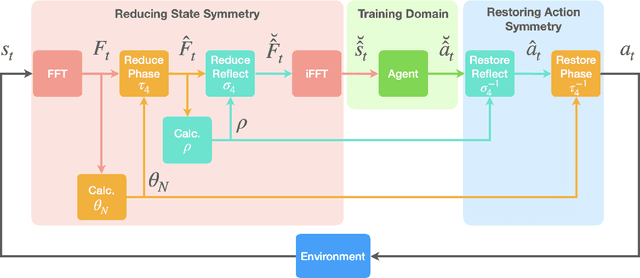
Deep reinforcement learning (RL) is a data-driven, model-free method capable of discovering complex control strategies for macroscopic objectives in high-dimensional systems, making its application towards flow control promising. Many systems of flow control interest possess symmetries that, when neglected, can significantly inhibit the learning and performance of a naive deep RL approach. Using a test-bed consisting of the Kuramoto-Sivashinsky Equation (KSE), equally spaced actuators, and a goal of minimizing dissipation and power cost, we demonstrate that by moving the deep RL problem to a symmetry-reduced space, we can alleviate limitations inherent in the naive application of deep RL. We demonstrate that symmetry-reduced deep RL yields improved data efficiency as well as improved control policy efficacy compared to policies found by naive deep RL. Interestingly, the policy learned by the the symmetry aware control agent drives the system toward an equilibrium state of the forced KSE that is connected by continuation to an equilibrium of the unforced KSE, despite having been given no explicit information regarding its existence. I.e., to achieve its goal, the RL algorithm discovers and stabilizes an equilibrium state of the system. Finally, we demonstrate that the symmetry-reduced control policy is robust to observation and actuation signal noise, as well as to system parameters it has not observed before.