Data-driven control of spatiotemporal chaos with reduced-order neural ODE-based models and reinforcement learning
Paper and Code
May 01, 2022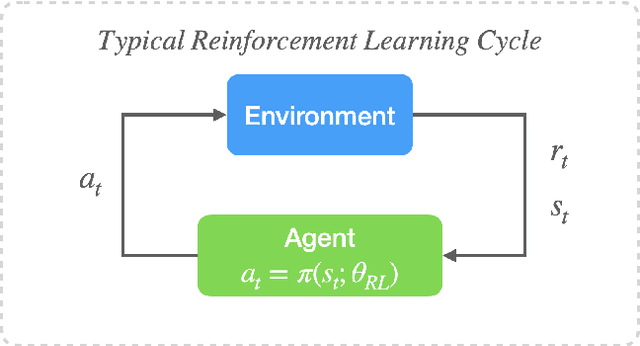

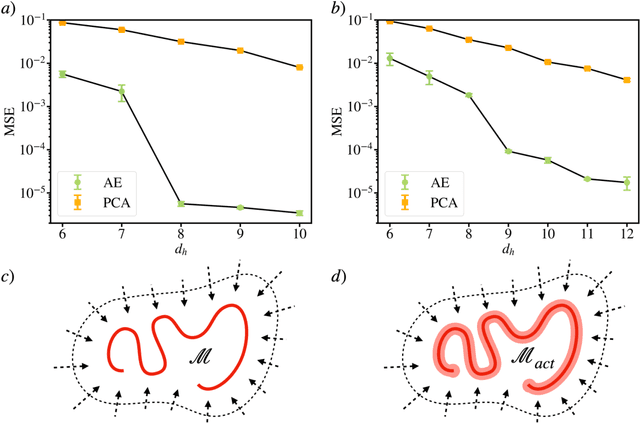
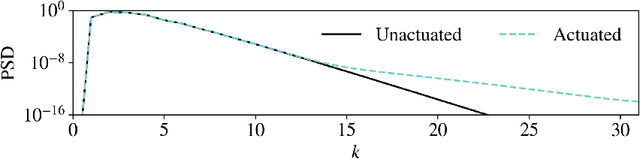
Deep reinforcement learning (RL) is a data-driven method capable of discovering complex control strategies for high-dimensional systems, making it promising for flow control applications. In particular, the present work is motivated by the goal of reducing energy dissipation in turbulent flows, and the example considered is the spatiotemporally chaotic dynamics of the Kuramoto-Sivashinsky equation (KSE). A major challenge associated with RL is that substantial training data must be generated by repeatedly interacting with the target system, making it costly when the system is computationally or experimentally expensive. We mitigate this challenge in a data-driven manner by combining dimensionality reduction via an autoencoder with a neural ODE framework to obtain a low-dimensional dynamical model from just a limited data set. We substitute this data-driven reduced-order model (ROM) in place of the true system during RL training to efficiently estimate the optimal policy, which can then be deployed on the true system. For the KSE actuated with localized forcing ("jets") at four locations, we demonstrate that we are able to learn a ROM that accurately captures the actuated dynamics as well as the underlying natural dynamics just from snapshots of the KSE experiencing random actuations. Using this ROM and a control objective of minimizing dissipation and power cost, we extract a control policy from it using deep RL. We show that the ROM-based control strategy translates well to the true KSE and highlight that the RL agent discovers and stabilizes an underlying forced equilibrium solution of the KSE system. We show that this forced equilibrium captured in the ROM and discovered through RL is related to an existing known equilibrium solution of the natural KSE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge