Symmetry reduction for deep reinforcement learning active control of chaotic spatiotemporal dynamics
Paper and Code
Apr 09, 2021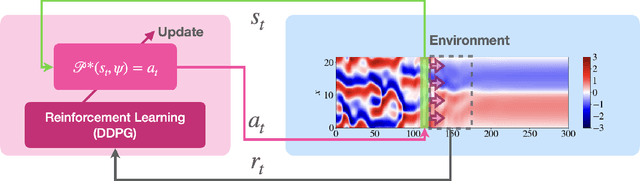
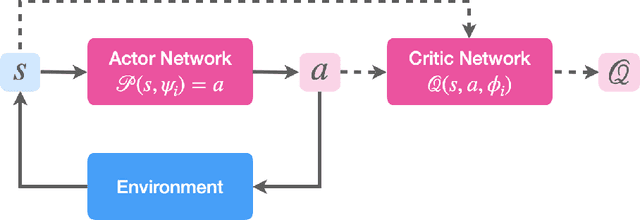
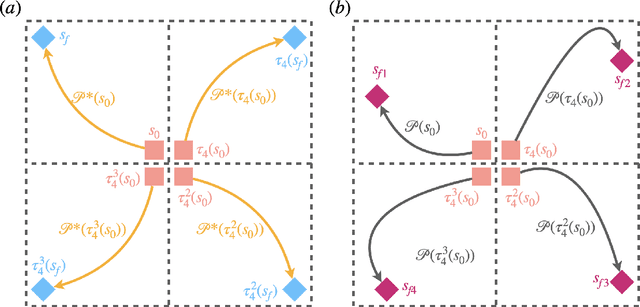
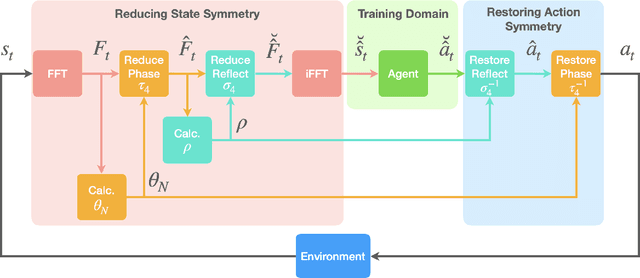
Deep reinforcement learning (RL) is a data-driven, model-free method capable of discovering complex control strategies for macroscopic objectives in high-dimensional systems, making its application towards flow control promising. Many systems of flow control interest possess symmetries that, when neglected, can significantly inhibit the learning and performance of a naive deep RL approach. Using a test-bed consisting of the Kuramoto-Sivashinsky Equation (KSE), equally spaced actuators, and a goal of minimizing dissipation and power cost, we demonstrate that by moving the deep RL problem to a symmetry-reduced space, we can alleviate limitations inherent in the naive application of deep RL. We demonstrate that symmetry-reduced deep RL yields improved data efficiency as well as improved control policy efficacy compared to policies found by naive deep RL. Interestingly, the policy learned by the the symmetry aware control agent drives the system toward an equilibrium state of the forced KSE that is connected by continuation to an equilibrium of the unforced KSE, despite having been given no explicit information regarding its existence. I.e., to achieve its goal, the RL algorithm discovers and stabilizes an equilibrium state of the system. Finally, we demonstrate that the symmetry-reduced control policy is robust to observation and actuation signal noise, as well as to system parameters it has not observed before.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge