One Filter to Deploy Them All: Robust Safety for Quadrupedal Navigation in Unknown Environments

As learning-based methods for legged robots rapidly grow in popularity, it is important that we can provide safety assurances efficiently across different controllers and environments. Existing works either rely on a priori knowledge of the environment and safety constraints to ensure system safety or provide assurances for a specific locomotion policy. To address these limitations, we propose an observation-conditioned reachability-based (OCR) safety-filter framework. Our key idea is to use an OCR value network (OCR-VN) that predicts the optimal control-theoretic safety value function for new failure regions and dynamic uncertainty during deployment time. Specifically, the OCR-VN facilitates rapid safety adaptation through two key components: a LiDAR-based input that allows the dynamic construction of safe regions in light of new obstacles and a disturbance estimation module that accounts for dynamics uncertainty in the wild. The predicted safety value function is used to construct an adaptive safety filter that overrides the nominal quadruped controller when necessary to maintain safety. Through simulation studies and hardware experiments on a Unitree Go1 quadruped, we demonstrate that the proposed framework can automatically safeguard a wide range of hierarchical quadruped controllers, adapts to novel environments, and is robust to unmodeled dynamics without a priori access to the controllers or environments - hence, "One Filter to Deploy Them All". The experiment videos can be found on the project website.

Language-Guided World Models: A Model-Based Approach to AI Control

Installing probabilistic world models into artificial agents opens an efficient channel for humans to communicate with and control these agents. In addition to updating agent policies, humans can modify their internal world models in order to influence their decisions. The challenge, however, is that currently existing world models are difficult for humans to adapt because they lack a natural communication interface. Aimed at addressing this shortcoming, we develop Language-Guided World Models (LWMs), which can capture environment dynamics by reading language descriptions. These models enhance agent communication efficiency, allowing humans to simultaneously alter their behavior on multiple tasks with concise language feedback. They also enable agents to self-learn from texts originally written to instruct humans. To facilitate the development of LWMs, we design a challenging benchmark based on the game of MESSENGER (Hanjie et al., 2021), requiring compositional generalization to new language descriptions and environment dynamics. Our experiments reveal that the current state-of-the-art Transformer architecture performs poorly on this benchmark, motivating us to design a more robust architecture. To showcase the practicality of our proposed LWMs, we simulate a scenario where these models augment the interpretability and safety of an agent by enabling it to generate and discuss plans with a human before execution. By effectively incorporating language feedback on the plan, the models boost the agent performance in the real environment by up to three times without collecting any interactive experiences in this environment.

Verification of Neural Reachable Tubes via Scenario Optimization and Conformal Prediction

Learning-based approaches for controlling safety-critical systems are rapidly growing in popularity; thus, it is important to assure their performance and safety. Hamilton-Jacobi (HJ) reachability analysis is a popular formal verification tool for providing such guarantees, since it can handle general nonlinear system dynamics, bounded adversarial system disturbances, and state and input constraints. However, its computational and memory complexity scales exponentially with the state dimension, making it intractable for large-scale systems. To overcome this challenge, neural approaches, such as DeepReach, have been used to synthesize reachable tubes and safety controllers for high-dimensional systems. However, verifying these neural reachable tubes remains challenging. In this work, we propose two verification methods, based on robust scenario optimization and conformal prediction, to provide probabilistic safety guarantees for neural reachable tubes. Our methods allow a direct trade-off between resilience to outlier errors in the neural tube, which are inevitable in a learning-based approach, and the strength of the probabilistic safety guarantee. Furthermore, we show that split conformal prediction, a widely used method in the machine learning community for uncertainty quantification, reduces to a scenario-based approach, making the two methods equivalent not only for verification of neural reachable tubes but also more generally. To our knowledge, our proof is the first in the literature to show a strong relationship between conformal prediction and scenario optimization. Finally, we propose an outlier-adjusted verification approach that uses the error distribution in neural reachable tubes to recover greater safe volumes. We demonstrate the efficacy of the proposed approaches for the high-dimensional problems of multi-vehicle collision avoidance and rocket landing with no-go zones.

Generating Formal Safety Assurances for High-Dimensional Reachability

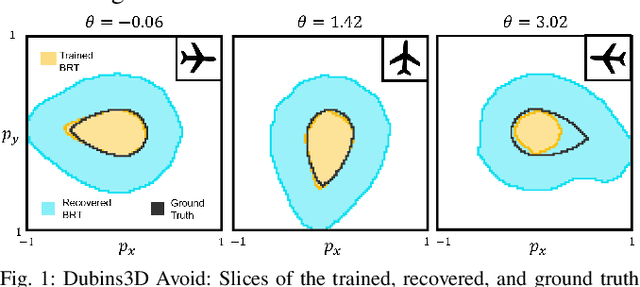
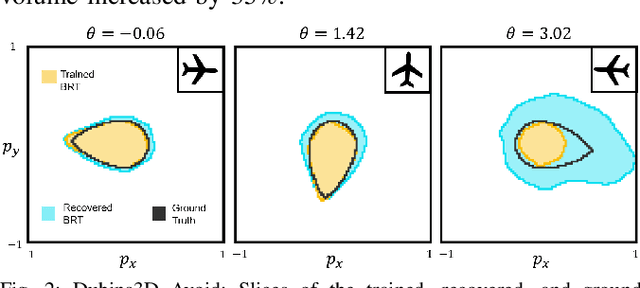
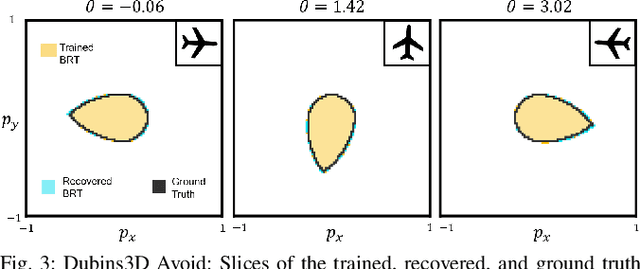
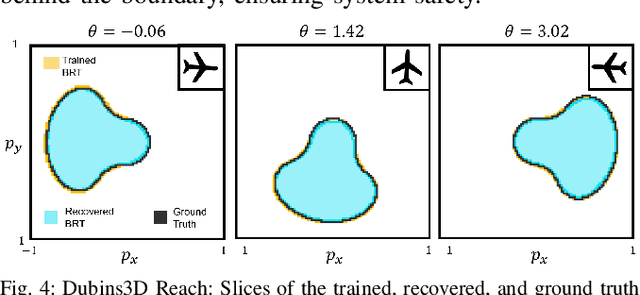
Providing formal safety and performance guarantees for autonomous systems is becoming increasingly important as they are integrated in our society. Hamilton-Jacobi (HJ) reachability analysis is a popular formal verification tool for providing these guarantees, since it can handle general nonlinear system dynamics, bounded adversarial system disturbances, and state and input constraints. However, it involves solving a PDE, whose computational and memory complexity scales exponentially with respect to the state dimensionality, making its direct use on large-scale systems intractable. A recently proposed method called DeepReach overcomes this challenge by leveraging a sinusoidal neural network PDE solver for high-dimensional reachability problems, whose computational requirements scale with the complexity of the underlying reachable tube rather than the state space dimension. Unfortunately, neural networks can make errors and thus the computed solution may not be safe, which falls short of achieving our overarching goal to provide formal safety assurances. In this work, we propose a method to compute an error bound for the DeepReach solution. This error bound can then be used for reachable tube correction, resulting in a provably safe approximation of the true reachable tube. We also propose a scenario optimization-based approach to compute this error bound for general nonlinear dynamical systems. We demonstrate the efficacy of the proposed approach in obtaining reachable tubes for high-dimensional rocket-landing and multi-vehicle collision-avoidance problems.