Generating Formal Safety Assurances for High-Dimensional Reachability

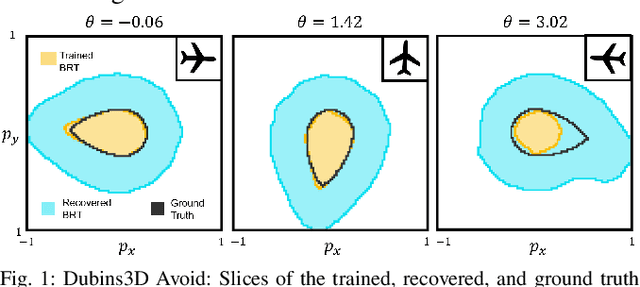
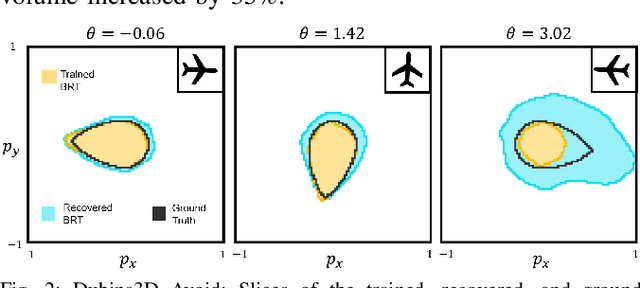
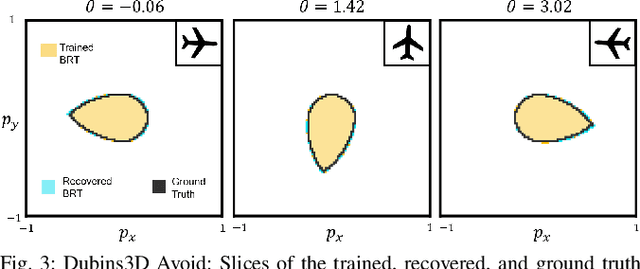
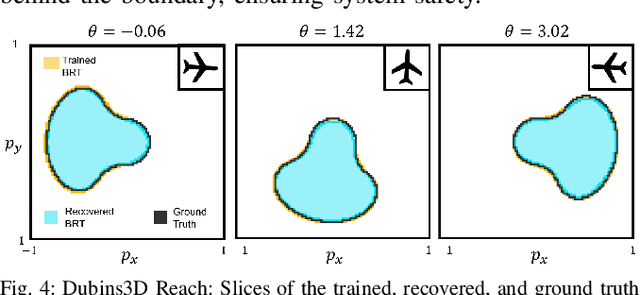
Providing formal safety and performance guarantees for autonomous systems is becoming increasingly important as they are integrated in our society. Hamilton-Jacobi (HJ) reachability analysis is a popular formal verification tool for providing these guarantees, since it can handle general nonlinear system dynamics, bounded adversarial system disturbances, and state and input constraints. However, it involves solving a PDE, whose computational and memory complexity scales exponentially with respect to the state dimensionality, making its direct use on large-scale systems intractable. A recently proposed method called DeepReach overcomes this challenge by leveraging a sinusoidal neural network PDE solver for high-dimensional reachability problems, whose computational requirements scale with the complexity of the underlying reachable tube rather than the state space dimension. Unfortunately, neural networks can make errors and thus the computed solution may not be safe, which falls short of achieving our overarching goal to provide formal safety assurances. In this work, we propose a method to compute an error bound for the DeepReach solution. This error bound can then be used for reachable tube correction, resulting in a provably safe approximation of the true reachable tube. We also propose a scenario optimization-based approach to compute this error bound for general nonlinear dynamical systems. We demonstrate the efficacy of the proposed approach in obtaining reachable tubes for high-dimensional rocket-landing and multi-vehicle collision-avoidance problems.