Supervised Dictionary Learning and Sparse Representation-A Review

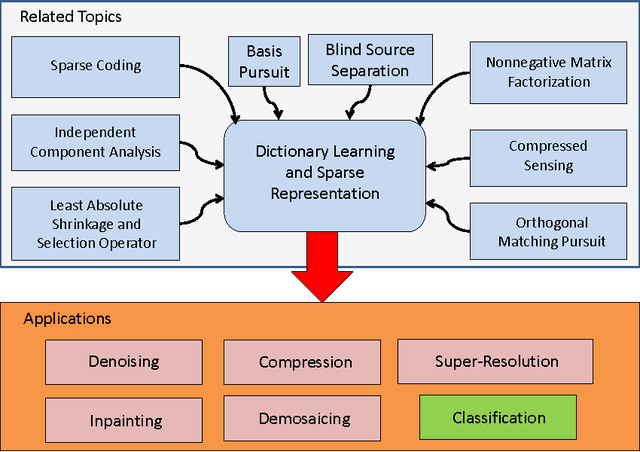
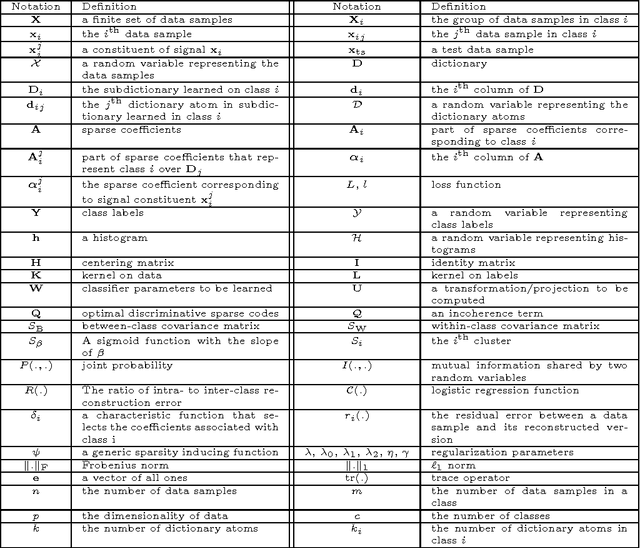
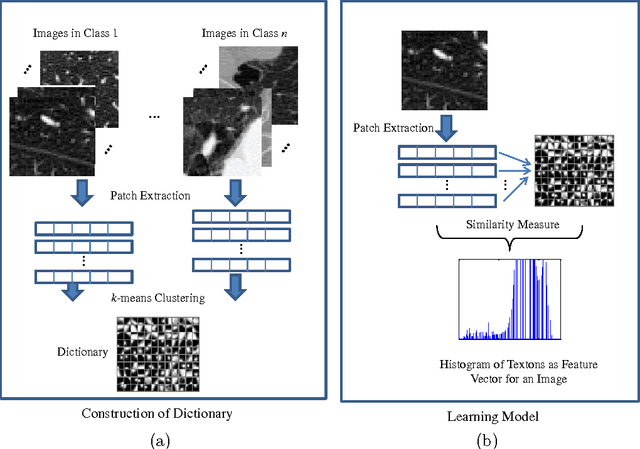
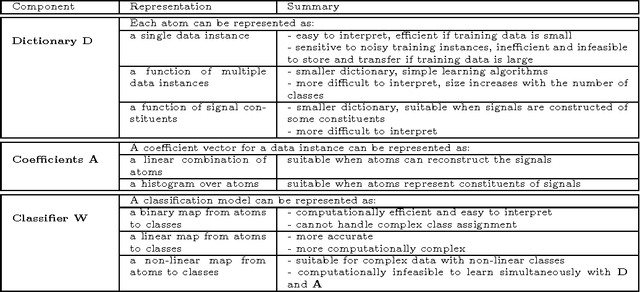
Dictionary learning and sparse representation (DLSR) is a recent and successful mathematical model for data representation that achieves state-of-the-art performance in various fields such as pattern recognition, machine learning, computer vision, and medical imaging. The original formulation for DLSR is based on the minimization of the reconstruction error between the original signal and its sparse representation in the space of the learned dictionary. Although this formulation is optimal for solving problems such as denoising, inpainting, and coding, it may not lead to optimal solution in classification tasks, where the ultimate goal is to make the learned dictionary and corresponding sparse representation as discriminative as possible. This motivated the emergence of a new category of techniques, which is appropriately called supervised dictionary learning and sparse representation (S-DLSR), leading to more optimal dictionary and sparse representation in classification tasks. Despite many research efforts for S-DLSR, the literature lacks a comprehensive view of these techniques, their connections, advantages and shortcomings. In this paper, we address this gap and provide a review of the recently proposed algorithms for S-DLSR. We first present a taxonomy of these algorithms into six categories based on the approach taken to include label information into the learning of the dictionary and/or sparse representation. For each category, we draw connections between the algorithms in this category and present a unified framework for them. We then provide guidelines for applied researchers on how to represent and learn the building blocks of an S-DLSR solution based on the problem at hand. This review provides a broad, yet deep, view of the state-of-the-art methods for S-DLSR and allows for the advancement of research and development in this emerging area of research.

Embed and Conquer: Scalable Embeddings for Kernel k-Means on MapReduce

The kernel $k$-means is an effective method for data clustering which extends the commonly-used $k$-means algorithm to work on a similarity matrix over complex data structures. The kernel $k$-means algorithm is however computationally very complex as it requires the complete data matrix to be calculated and stored. Further, the kernelized nature of the kernel $k$-means algorithm hinders the parallelization of its computations on modern infrastructures for distributed computing. In this paper, we are defining a family of kernel-based low-dimensional embeddings that allows for scaling kernel $k$-means on MapReduce via an efficient and unified parallelization strategy. Afterwards, we propose two methods for low-dimensional embedding that adhere to our definition of the embedding family. Exploiting the proposed parallelization strategy, we present two scalable MapReduce algorithms for kernel $k$-means. We demonstrate the effectiveness and efficiency of the proposed algorithms through an empirical evaluation on benchmark data sets.

Greedy Column Subset Selection for Large-scale Data Sets

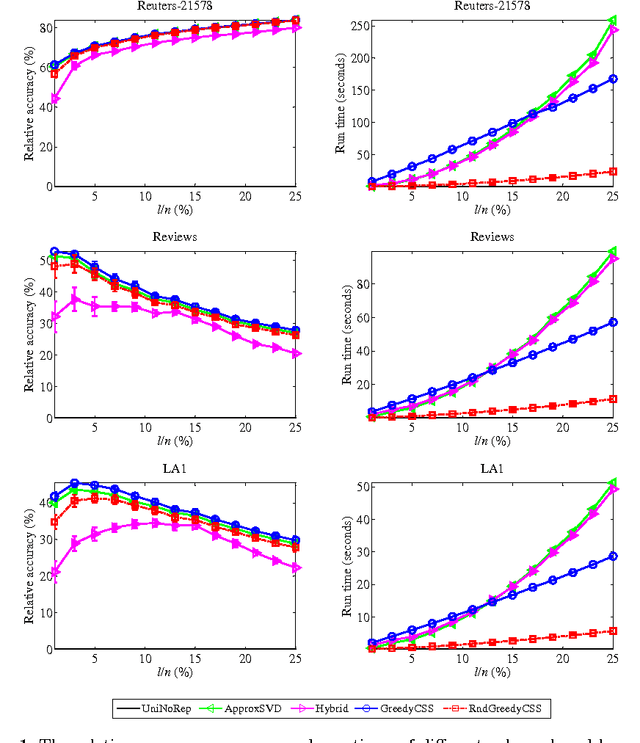
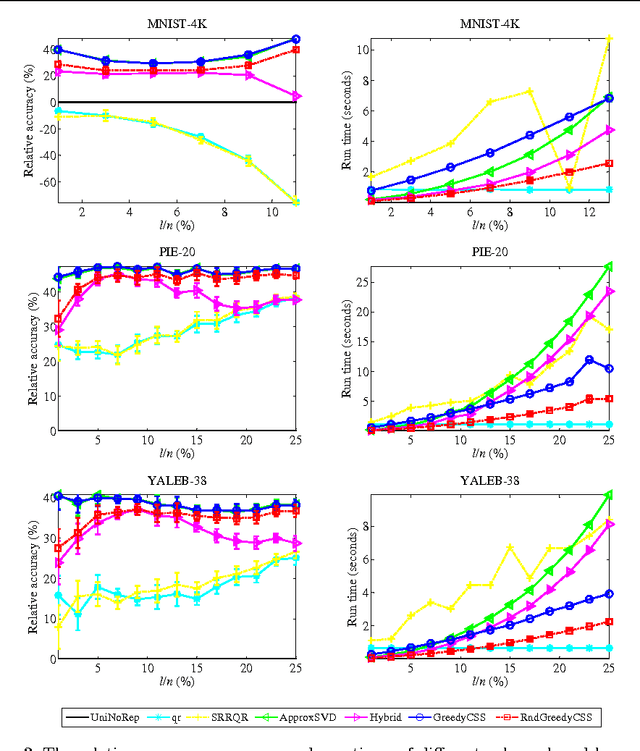
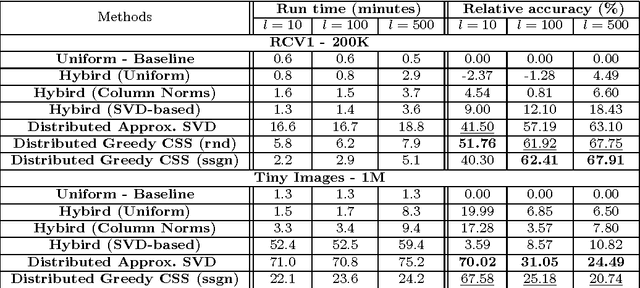
In today's information systems, the availability of massive amounts of data necessitates the development of fast and accurate algorithms to summarize these data and represent them in a succinct format. One crucial problem in big data analytics is the selection of representative instances from large and massively-distributed data, which is formally known as the Column Subset Selection (CSS) problem. The solution to this problem enables data analysts to understand the insights of the data and explore its hidden structure. The selected instances can also be used for data preprocessing tasks such as learning a low-dimensional embedding of the data points or computing a low-rank approximation of the corresponding matrix. This paper presents a fast and accurate greedy algorithm for large-scale column subset selection. The algorithm minimizes an objective function which measures the reconstruction error of the data matrix based on the subset of selected columns. The paper first presents a centralized greedy algorithm for column subset selection which depends on a novel recursive formula for calculating the reconstruction error of the data matrix. The paper then presents a MapReduce algorithm which selects a few representative columns from a matrix whose columns are massively distributed across several commodity machines. The algorithm first learns a concise representation of all columns using random projection, and it then solves a generalized column subset selection problem at each machine in which a subset of columns are selected from the sub-matrix on that machine such that the reconstruction error of the concise representation is minimized. The paper demonstrates the effectiveness and efficiency of the proposed algorithm through an empirical evaluation on benchmark data sets.

A Fast Greedy Algorithm for Generalized Column Subset Selection

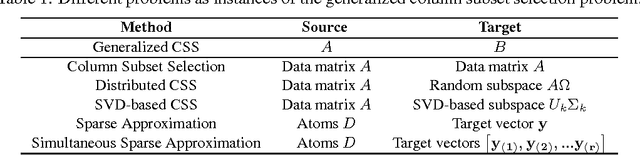
This paper defines a generalized column subset selection problem which is concerned with the selection of a few columns from a source matrix A that best approximate the span of a target matrix B. The paper then proposes a fast greedy algorithm for solving this problem and draws connections to different problems that can be efficiently solved using the proposed algorithm.

Discriminative Density-ratio Estimation

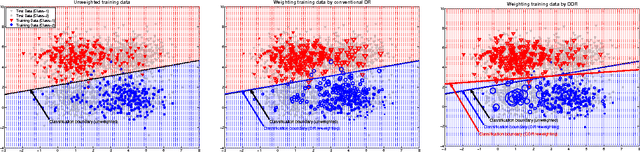
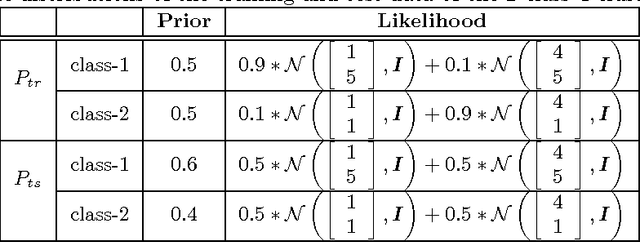
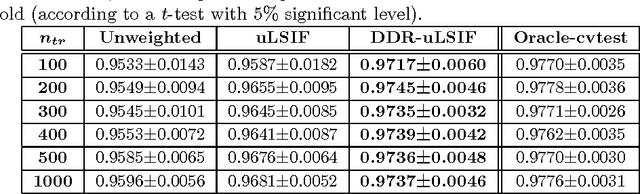
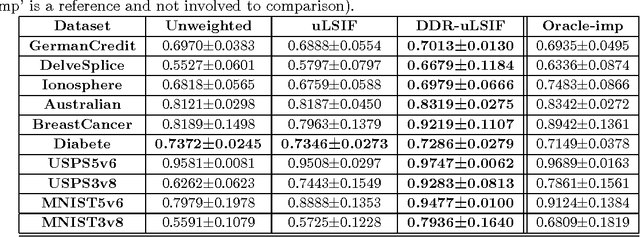
The covariate shift is a challenging problem in supervised learning that results from the discrepancy between the training and test distributions. An effective approach which recently drew a considerable attention in the research community is to reweight the training samples to minimize that discrepancy. In specific, many methods are based on developing Density-ratio (DR) estimation techniques that apply to both regression and classification problems. Although these methods work well for regression problems, their performance on classification problems is not satisfactory. This is due to a key observation that these methods focus on matching the sample marginal distributions without paying attention to preserving the separation between classes in the reweighted space. In this paper, we propose a novel method for Discriminative Density-ratio (DDR) estimation that addresses the aforementioned problem and aims at estimating the density-ratio of joint distributions in a class-wise manner. The proposed algorithm is an iterative procedure that alternates between estimating the class information for the test data and estimating new density ratio for each class. To incorporate the estimated class information of the test data, a soft matching technique is proposed. In addition, we employ an effective criterion which adopts mutual information as an indicator to stop the iterative procedure while resulting in a decision boundary that lies in a sparse region. Experiments on synthetic and benchmark datasets demonstrate the superiority of the proposed method in terms of both accuracy and robustness.