Version Age of Information with Contact Mobility in Gossip Networks

A gossip network is considered in which a source node updates its status while other nodes in the network aim at keeping track of it as it varies over time. Information gets disseminated by the source sending status updates to the nodes, and the nodes gossiping with each other. In addition, the nodes in the network are mobile, and can move to other nodes to get information, which we term contact mobility. The goal for the nodes is to remain as fresh as possible, i.e., to have the same information as the source's. To evaluate the freshness of information, we use the Version Age-of-Information (VAoI) metric, defined as the difference between the version of information available at a given node and that at the source. We analyze the effect of contact mobility on information dissemination in the gossip network using a Stochastic Hybrid System (SHS) framework for different topologies and mobility scalings with increasing number of nodes. It is shown that with the presence of contact mobility the freshness of the network improves in both ends of the network connectivity spectrum: disconnected and fully connected gossip networks. We mathematically analyze the average version age scalings and validate our theoretical results via simulations. Finally, we incorporate the cost of mobility for the network by formulating and solving an optimization problem that minimizes a weighted sum of version age and mobility cost. Our results show that contact mobility, with optimized mobility cost, improves the average version age in the network.

Status Updating with Time Stamp Errors

A status updating system is considered in which multiple processes are sampled and transmitted through a shared channel. Each process has its dedicated server that processes its samples before time stamping them for transmission. Time stamps, however, are prone to errors, and hence the status updates received may not be credible. Our setting models the time stamp error rate as a function of the servers' busy times. Hence, to reduce errors and enhance credibility, servers need to process samples on a relatively prolonged schedule. This, however, deteriorates timeliness, which is captured through the age of information (AoI) metric. An optimization problem is formulated whose goal to characterize the optimal processes' schedule and sampling instances to achieve the optimal trade-off between timeliness and credibility. The problem is first solved for a single process setting, where it is shown that a threshold-based sleep-wake schedule is optimal, in which the server wakes up and is allowed to process newly incoming samples only if the AoI surpasses a certain threshold that depends on the required timeliness-credibility trade-off. Such insights are then extended to the multi-process setting, where two main scheduling and sleep-wake policies, namely round-robin scheduling with threshold-waiting and asymmetric scheduling with zero-waiting, are introduced and analyzed.

RCC-PFL: Robust Client Clustering under Noisy Labels in Personalized Federated Learning

We address the problem of cluster identity estimation in a personalized federated learning (PFL) setting in which users aim to learn different personal models. The backbone of effective learning in such a setting is to cluster users into groups whose objectives are similar. A typical approach in the literature is to achieve this by training users' data on different proposed personal models and assign them to groups based on which model achieves the lowest value of the users' loss functions. This process is to be done iteratively until group identities converge. A key challenge in such a setting arises when users have noisy labeled data, which may produce misleading values of their loss functions, and hence lead to ineffective clustering. To overcome this challenge, we propose a label-agnostic data similarity-based clustering algorithm, coined RCC-PFL, with three main advantages: the cluster identity estimation procedure is independent from the training labels; it is a one-shot clustering algorithm performed prior to the training; and it requires fewer communication rounds and less computation compared to iterative-based clustering methods. We validate our proposed algorithm using various models and datasets and show that it outperforms multiple baselines in terms of average accuracy and variance reduction.

Data Similarity-Based One-Shot Clustering for Multi-Task Hierarchical Federated Learning

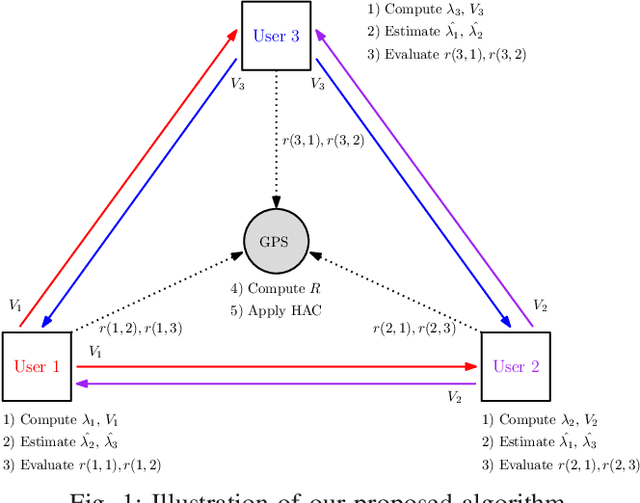
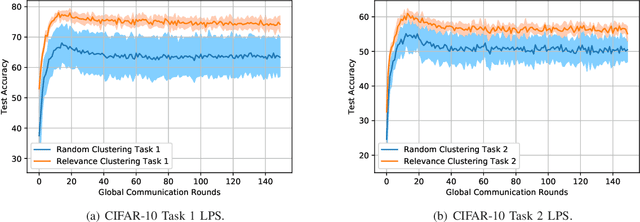
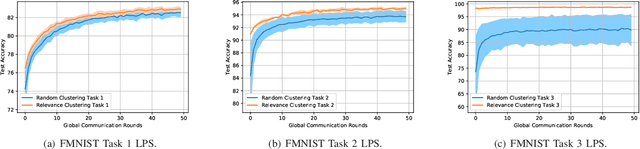
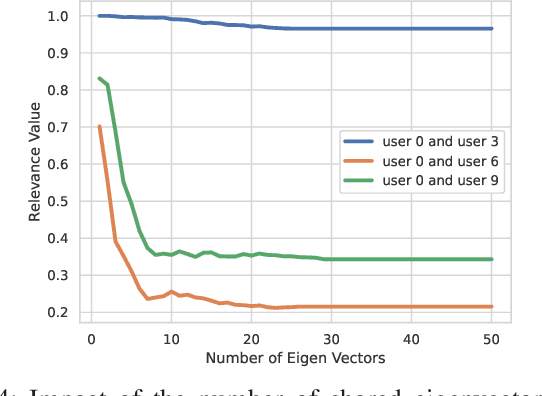
We address the problem of cluster identity estimation in a hierarchical federated learning setting in which users work toward learning different tasks. To overcome the challenge of task heterogeneity, users need to be grouped in a way such that users with the same task are in the same group, conducting training together, while sharing the weights of feature extraction layers with the other groups. Toward that end, we propose a one-shot clustering algorithm that can effectively identify and group users based on their data similarity. This enables more efficient collaboration and sharing of a common layer representation within the federated learning system. Our proposed algorithm not only enhances the clustering process, but also overcomes challenges related to privacy concerns, communication overhead, and the need for prior knowledge about learning models or loss function behaviors. We validate our proposed algorithm using various datasets such as CIFAR-10 and Fashion MNIST, and show that it outperforms the baseline in terms of accuracy and variance reduction.

Age and Value of Information Optimization for Systems with Multi-Class Updates

Received samples of a stochastic process are processed by a server for delivery as updates to a monitor. Each sample belongs to a class that specifies a distribution for its processing time and a function that describes how the value of the processed update decays with age at the monitor. The class of a sample is identified when the processed update is delivered. The server implements a form of M/G/1/1 blocking queue; samples arriving at a busy server are discarded and samples arriving at an idle server are subject to an admission policy that depends on the age and class of the prior delivered update. For the delivered updates, we characterize the average age of information (AoI) and average value of information (VoI). We derive the optimal stationary policy that minimizes the convex combination of the AoI and (negative) VoI. It is shown that the policy has a threshold structure, in which a new sample is allowed to arrive to the server only if the previous update's age and value difference surpasses a certain threshold that depends on the specifics of the value function and system statistics.

Private Status Updating with Erasures: A Case for Retransmission Without Resampling

A status updating system is considered in which a source updates a destination over an erasure channel. The utility of the updates is measured through a function of their age-of-information (AoI), which assesses their freshness. Correlated with the status updates is another process that needs to be kept private from the destination. Privacy is measured through a leakage function that depends on the amount and time of the status updates received: stale updates are more private than fresh ones. Different from most of the current AoI literature, a post-sampling waiting time is introduced in order to provide a privacy cover at the expense of AoI. More importantly, it is also shown that, depending on the leakage budget and the channel statistics, it can be useful to retransmit stale status updates following erasure events without resampling fresh ones.

Delay Sensitive Hierarchical Federated Learning with Stochastic Local Updates

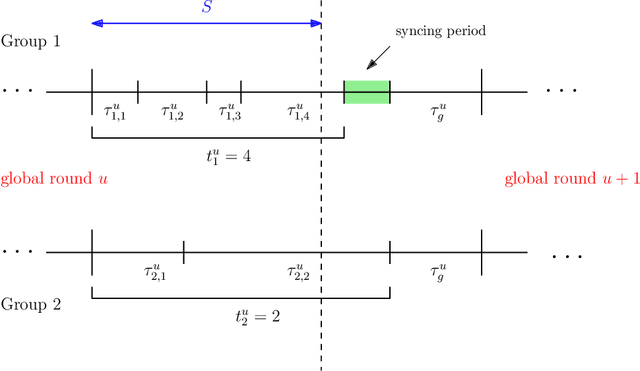
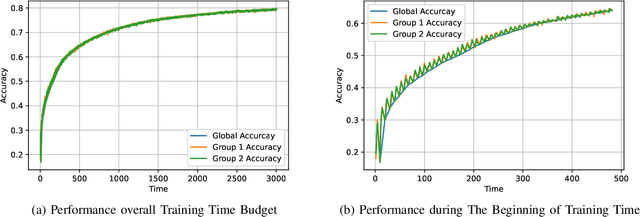
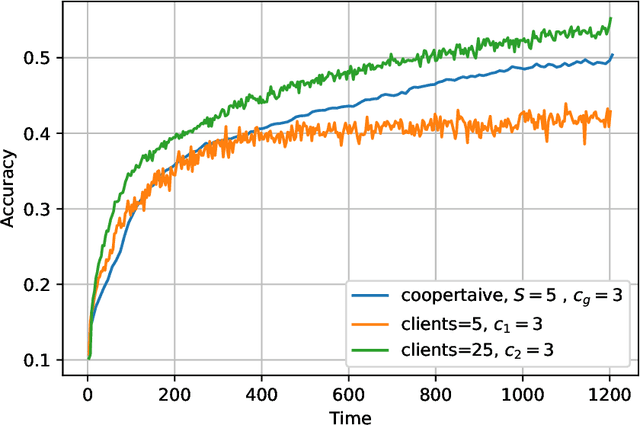
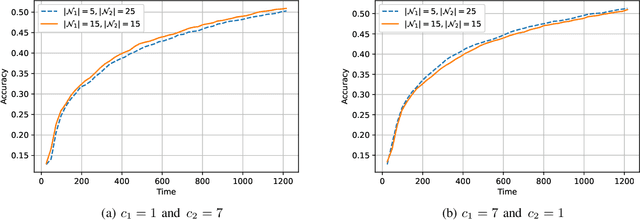
The impact of local averaging on the performance of federated learning (FL) systems is studied in the presence of communication delay between the clients and the parameter server. To minimize the effect of delay, clients are assigned into different groups, each having its own local parameter server (LPS) that aggregates its clients' models. The groups' models are then aggregated at a global parameter server (GPS) that only communicates with the LPSs. Such setting is known as hierarchical FL (HFL). Different from most works in the literature, the number of local and global communication rounds in our work is randomly determined by the (different) delays experienced by each group of clients. Specifically, the number of local averaging rounds are tied to a wall-clock time period coined the sync time $S$, after which the LPSs synchronize their models by sharing them with the GPS. Such sync time $S$ is then reapplied until a global wall-clock time is exhausted.

Timely Multi-Process Estimation with Erasures

We consider a multi-process remote estimation system observing $K$ independent Ornstein-Uhlenbeck processes. In this system, a shared sensor samples the $K$ processes in such a way that the long-term average sum mean square error (MSE) is minimized. The sensor operates under a total sampling frequency constraint $f_{\max}$ and samples the processes according to a Maximum-Age-First (MAF) schedule. The samples from all processes consume random processing delays, and then are transmitted over an erasure channel with probability $\epsilon$. Aided by optimal structural results, we show that the optimal sampling policy, under some conditions, is a \emph{threshold policy}. We characterize the optimal threshold and the corresponding optimal long-term average sum MSE as a function of $K$, $f_{\max}$, $\epsilon$, and the statistical properties of the observed processes.

Timely Updating with Intermittent Energy and Data for Multiple Sources over Erasure Channels

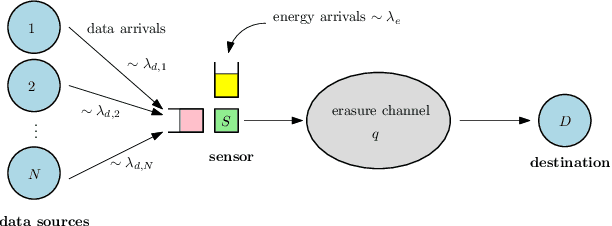
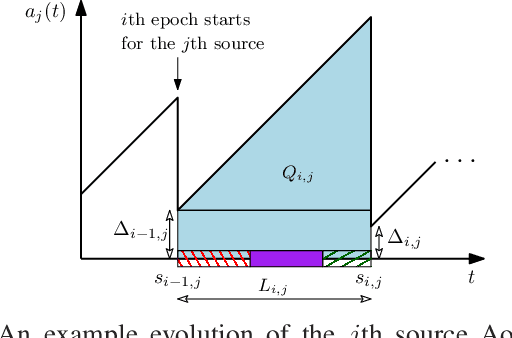
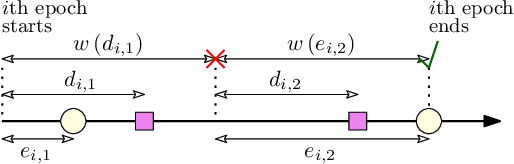
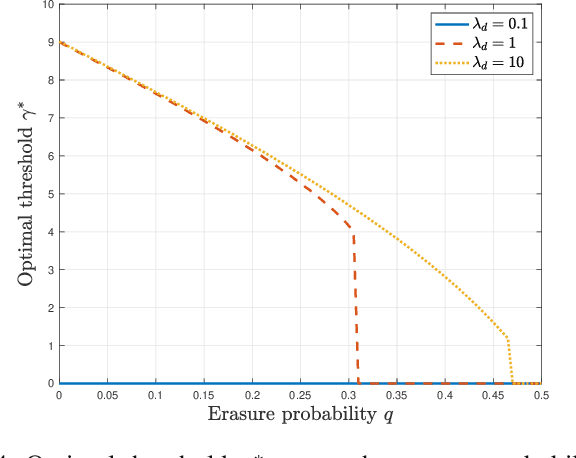
A status updating system is considered in which multiple data sources generate packets to be delivered to a destination through a shared energy harvesting sensor. Only one source's data, when available, can be transmitted by the sensor at a time, subject to energy availability. Transmissions are prune to erasures, and each successful transmission constitutes a status update for its corresponding source at the destination. The goal is to schedule source transmissions such that the collective long-term average age-of-information (AoI) is minimized. AoI is defined as the time elapsed since the latest successfully-received data has been generated at its source. To solve this problem, the case with a single source is first considered, with a focus on threshold waiting policies, in which the sensor attempts transmission only if the time until both energy and data are available grows above a certain threshold. The distribution of the AoI is fully characterized under such a policy. This is then used to analyze the performance of the multiple sources case under maximum-age-first scheduling, in which the sensor's resources are dedicated to the source with the maximum AoI at any given time. The achievable collective long-term average AoI is derived in closed-form. Multiple numerical evaluations are demonstrated to show how the optimal threshold value behaves as a function of the system parameters, and showcase the benefits of a threshold-based waiting policy with intermittent energy and data arrivals.

Timely Status Updating Over Erasure Channels Using an Energy Harvesting Sensor: Single and Multiple Sources

A status updating system is considered in which data from multiple sources are sampled by an energy harvesting sensor and transmitted to a remote destination through an erasure channel. The goal is to deliver status updates of all sources in a timely manner, such that the cumulative long-term average age-of-information (AoI) is minimized. The AoI for each source is defined as the time elapsed since the generation time of the latest successful status update received at the destination from that source. Transmissions are subject to energy availability, which arrives in units according to a Poisson process, with each energy unit capable of carrying out one transmission from only one source. The sensor is equipped with a unit-sized battery to save the incoming energy. A scheduling policy is designed in order to determine which source is sampled using the available energy. The problem is studied in two main settings: no erasure status feedback, and perfect instantaneous feedback.