Delay Sensitive Hierarchical Federated Learning with Stochastic Local Updates
Paper and Code
Feb 09, 2023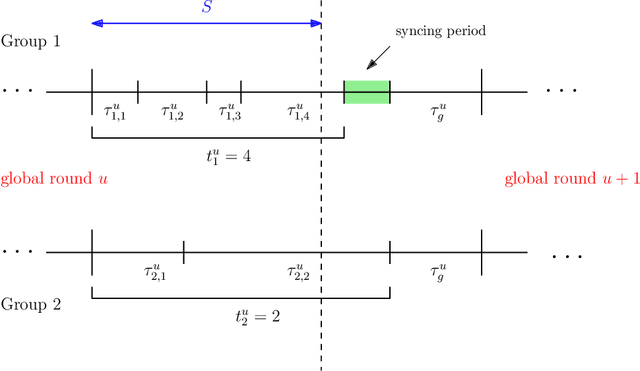
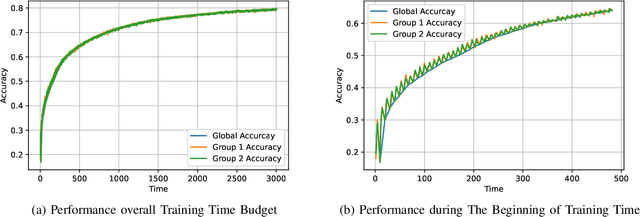
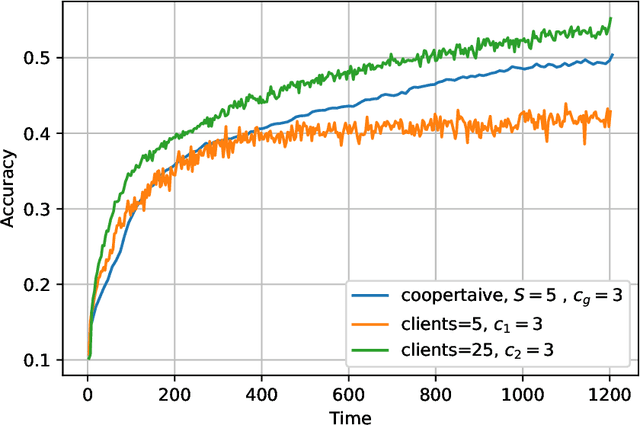
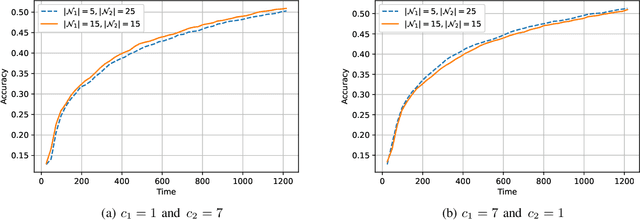
The impact of local averaging on the performance of federated learning (FL) systems is studied in the presence of communication delay between the clients and the parameter server. To minimize the effect of delay, clients are assigned into different groups, each having its own local parameter server (LPS) that aggregates its clients' models. The groups' models are then aggregated at a global parameter server (GPS) that only communicates with the LPSs. Such setting is known as hierarchical FL (HFL). Different from most works in the literature, the number of local and global communication rounds in our work is randomly determined by the (different) delays experienced by each group of clients. Specifically, the number of local averaging rounds are tied to a wall-clock time period coined the sync time $S$, after which the LPSs synchronize their models by sharing them with the GPS. Such sync time $S$ is then reapplied until a global wall-clock time is exhausted.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge