Optimizing Wireless Discontinuous Reception via MAC Signaling Learning

We present a Reinforcement Learning (RL) approach to the problem of controlling the Discontinuous Reception (DRX) policy from a Base Transceiver Station (BTS) in a cellular network. We do so by means of optimally timing the transmission of fast Layer-2 signaling messages (a.k.a. Medium Access Layer (MAC) Control Elements (CEs) as specified in 5G New Radio). Unlike more conventional approaches to DRX optimization, which rely on fine-tuning the values of DRX timers, we assess the gains that can be obtained solely by means of this MAC CE signalling. For the simulation part, we concentrate on traffic types typically encountered in Extended Reality (XR) applications, where the need for battery drain minimization and overheating mitigation are particularly pressing. Both 3GPP 5G New Radio (5G NR) compliant and non-compliant ("beyond 5G") MAC CEs are considered. Our simulation results show that our proposed technique strikes an improved trade-off between latency and energy savings as compared to conventional timer-based approaches that are characteristic of most current implementations. Specifically, our RL-based policy can nearly halve the active time for a single User Equipment (UE) with respect to a na\"ive MAC CE transmission policy, and still achieve near 20% active time reduction for 9 simultaneously served UEs.

A Weighted Autoencoder-Based Approach to Downlink NOMA Constellation Design

End-to-end design of communication systems using deep autoencoders (AEs) is gaining attention due to its flexibility and excellent performance. Besides single-user transmission, AE-based design is recently explored in multi-user setup, e.g., for designing constellations for non-orthogonal multiple access (NOMA). In this paper, we further advance the design of AE-based downlink NOMA by introducing weighted loss function in the AE training. By changing the weight coefficients, one can flexibly tune the constellation design to balance error probability of different users, without relying on explicit information about their channel quality. Combined with the SICNet decoder, we demonstrate a significant improvement in achievable levels and flexible control of error probability of different users using the proposed weighted AE-based framework.

Beam Aware Stochastic Multihop Routing for Flying Ad-hoc Networks

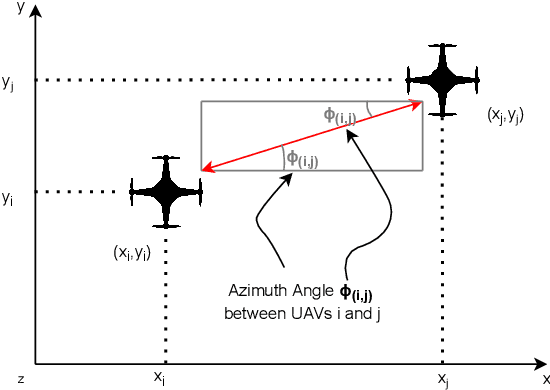
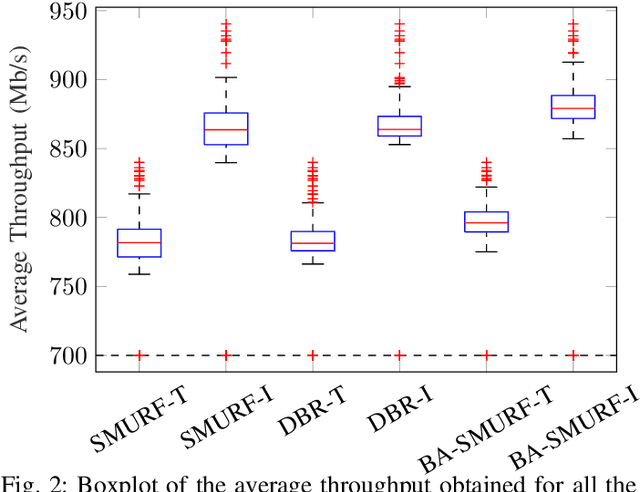
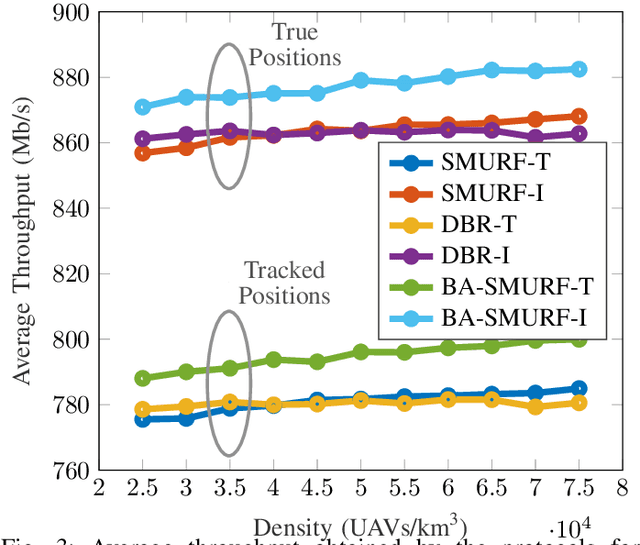
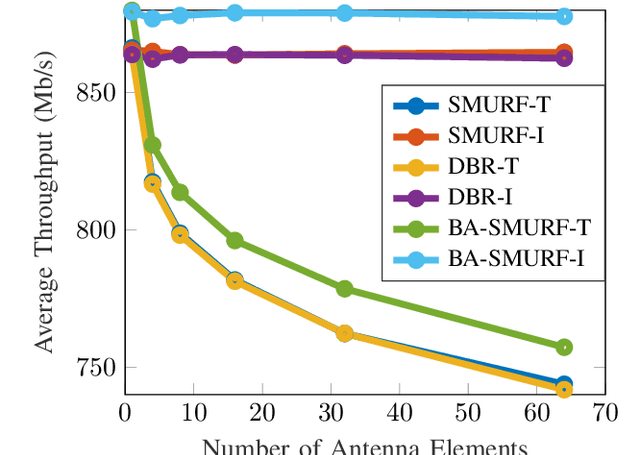
Routing is a crucial component in the design of Flying Ad-Hoc Networks (FANETs). State of the art routing solutions exploit the position of Unmanned Aerial Vehicles (UAVs) and their mobility information to determine the existence of links between them, but this information is often unreliable, as the topology of FANETs can change quickly and unpredictably. In order to improve the tracking performance, the uncertainty introduced by imperfect measurements and tracking algorithms needs to be accounted for in the routing. Another important element to consider is beamforming, which can reduce interference, but requires accurate channel and position information to work. In this work, we present the Beam Aware Stochastic Multihop Routing for FANETs (BA-SMURF), a Software-Defined Networking (SDN) routing scheme that takes into account the positioning uncertainty and beamforming design to find the most reliable routes in a FANET. Our simulation results show that joint consideration of the beamforming and routing can provide a 5% throughput improvement with respect to the state of the art.

Locally Differentially-Private Randomized Response for Discrete Distribution Learning

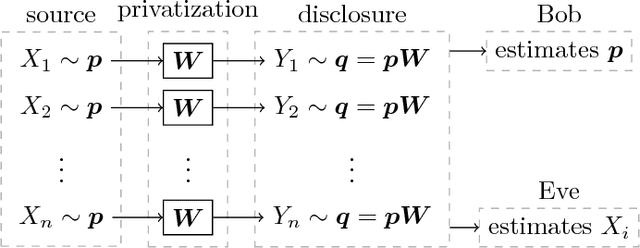
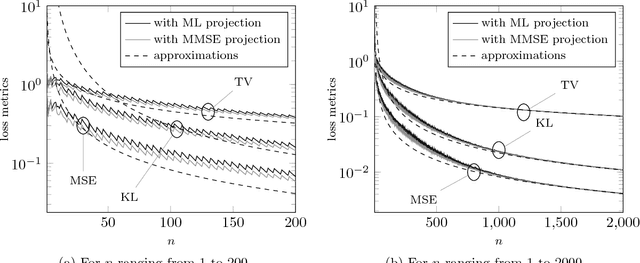
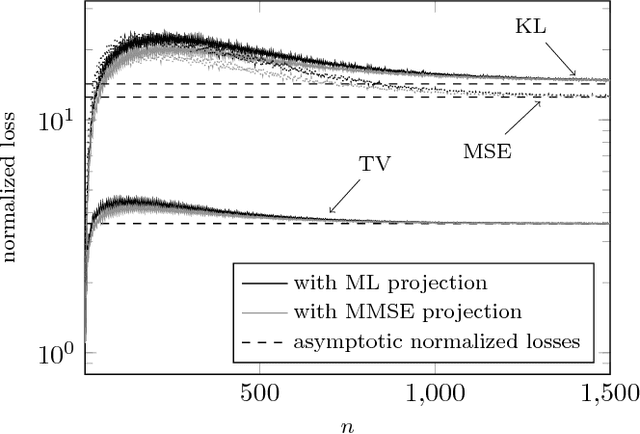
We consider a setup in which confidential i.i.d. samples $X_1,\dotsc,X_n$ from an unknown finite-support distribution $\boldsymbol{p}$ are passed through $n$ copies of a discrete privatization channel (a.k.a. mechanism) producing outputs $Y_1,\dotsc,Y_n$. The channel law guarantees a local differential privacy of $\epsilon$. Subject to a prescribed privacy level $\epsilon$, the optimal channel should be designed such that an estimate of the source distribution based on the channel outputs $Y_1,\dotsc,Y_n$ converges as fast as possible to the exact value $\boldsymbol{p}$. For this purpose we study the convergence to zero of three distribution distance metrics: $f$-divergence, mean-squared error and total variation. We derive the respective normalized first-order terms of convergence (as $n\to\infty$), which for a given target privacy $\epsilon$ represent a rule-of-thumb factor by which the sample size must be augmented so as to achieve the same estimation accuracy as that of a non-randomizing channel. We formulate the privacy-fidelity trade-off problem as being that of minimizing said first-order term under a privacy constraint $\epsilon$. We further identify a scalar quantity that captures the essence of this trade-off, and prove bounds and data-processing inequalities on this quantity. For some specific instances of the privacy-fidelity trade-off problem, we derive inner and outer bounds on the optimal trade-off curve.