Adler J. Perotte
Causal Estimation with Functional Confounders
Feb 17, 2021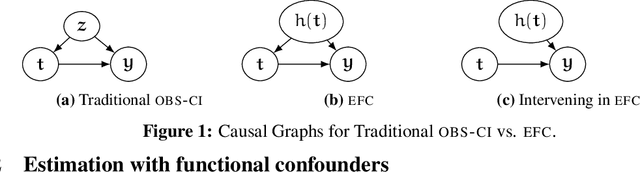
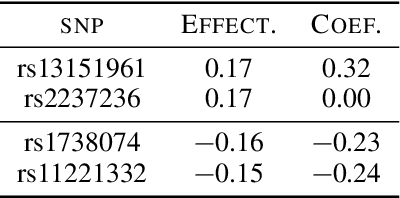
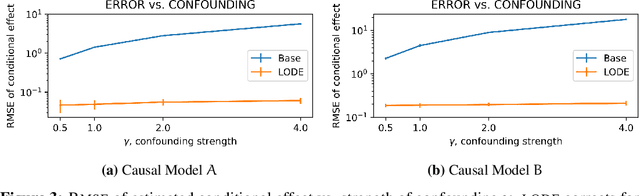
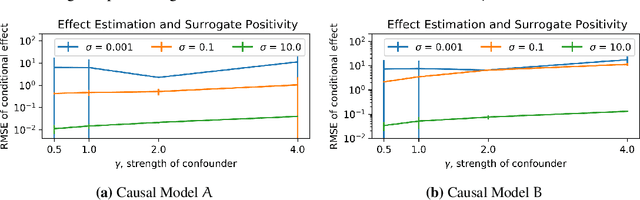
Abstract:Causal inference relies on two fundamental assumptions: ignorability and positivity. We study causal inference when the true confounder value can be expressed as a function of the observed data; we call this setting estimation with functional confounders (EFC). In this setting, ignorability is satisfied, however positivity is violated, and causal inference is impossible in general. We consider two scenarios where causal effects are estimable. First, we discuss interventions on a part of the treatment called functional interventions and a sufficient condition for effect estimation of these interventions called functional positivity. Second, we develop conditions for nonparametric effect estimation based on the gradient fields of the functional confounder and the true outcome function. To estimate effects under these conditions, we develop Level-set Orthogonal Descent Estimation (LODE). Further, we prove error bounds on LODE's effect estimates, evaluate our methods on simulated and real data, and empirically demonstrate the value of EFC.
X-CAL: Explicit Calibration for Survival Analysis
Jan 13, 2021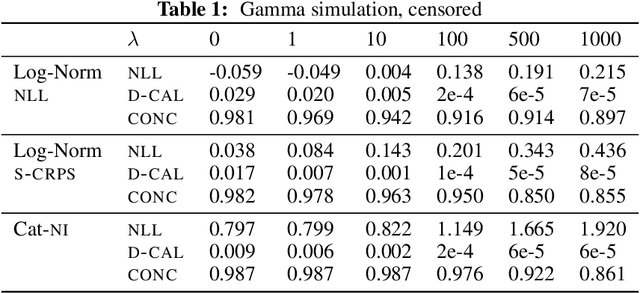
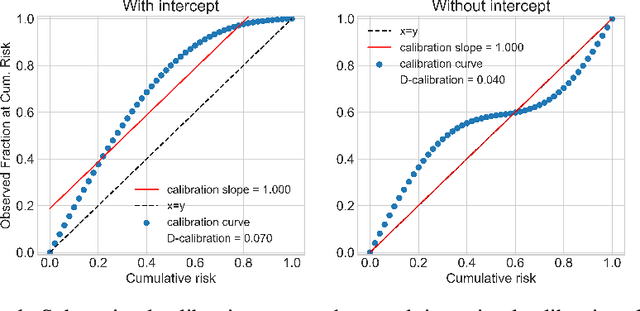
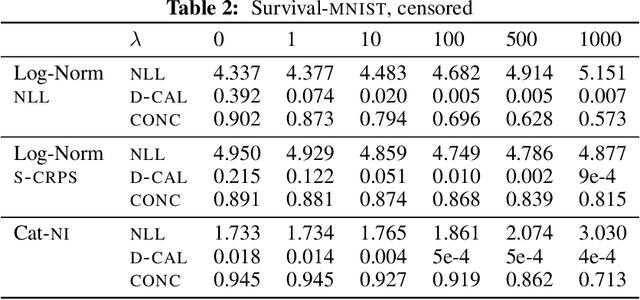
Abstract:Survival analysis models the distribution of time until an event of interest, such as discharge from the hospital or admission to the ICU. When a model's predicted number of events within any time interval is similar to the observed number, it is called well-calibrated. A survival model's calibration can be measured using, for instance, distributional calibration (D-CALIBRATION) [Haider et al., 2020] which computes the squared difference between the observed and predicted number of events within different time intervals. Classically, calibration is addressed in post-training analysis. We develop explicit calibration (X-CAL), which turns D-CALIBRATION into a differentiable objective that can be used in survival modeling alongside maximum likelihood estimation and other objectives. X-CAL allows practitioners to directly optimize calibration and strike a desired balance between predictive power and calibration. In our experiments, we fit a variety of shallow and deep models on simulated data, a survival dataset based on MNIST, on length-of-stay prediction using MIMIC-III data, and on brain cancer data from The Cancer Genome Atlas. We show that the models we study can be miscalibrated. We give experimental evidence on these datasets that X-CAL improves D-CALIBRATION without a large decrease in concordance or likelihood.
The Counterfactual $χ$-GAN
Jan 09, 2020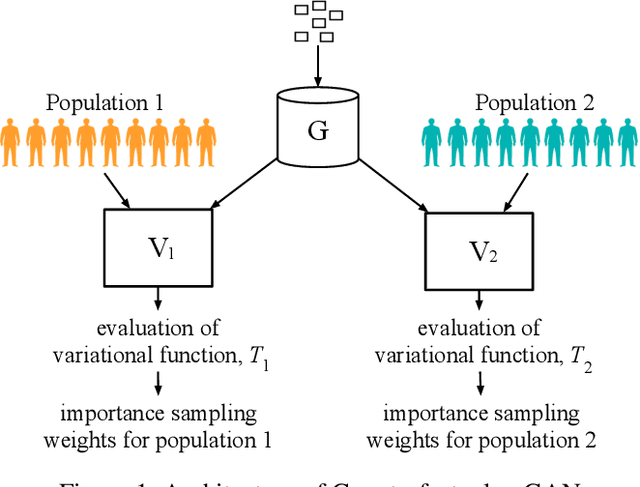
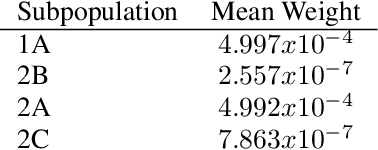
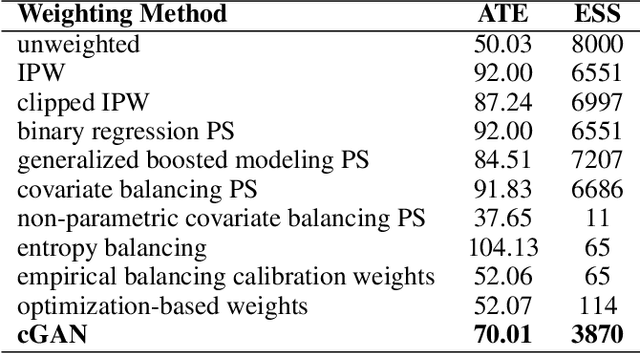
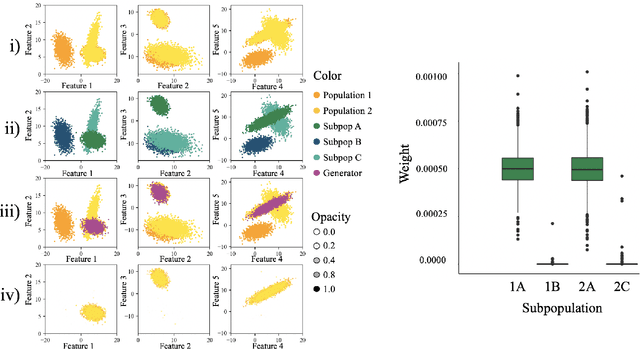
Abstract:Causal inference often relies on the counterfactual framework, which requires that treatment assignment is independent of the outcome, known as strong ignorability. Approaches to enforcing strong ignorability in causal analyses of observational data include weighting and matching methods. Effect estimates, such as the average treatment effect (ATE), are then estimated as expectations under the reweighted or matched distribution, P . The choice of P is important and can impact the interpretation of the effect estimate and the variance of effect estimates. In this work, instead of specifying P, we learn a distribution that simultaneously maximizes coverage and minimizes variance of ATE estimates. In order to learn this distribution, this research proposes a generative adversarial network (GAN)-based model called the Counterfactual $\chi$-GAN (cGAN), which also learns feature-balancing weights and supports unbiased causal estimation in the absence of unobserved confounding. Our model minimizes the Pearson $\chi^2$ divergence, which we show simultaneously maximizes coverage and minimizes the variance of importance sampling estimates. To our knowledge, this is the first such application of the Pearson $\chi^2$ divergence. We demonstrate the effectiveness of cGAN in achieving feature balance relative to established weighting methods in simulation and with real-world medical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge