Amelia J. Averitt
The Counterfactual $χ$-GAN
Jan 09, 2020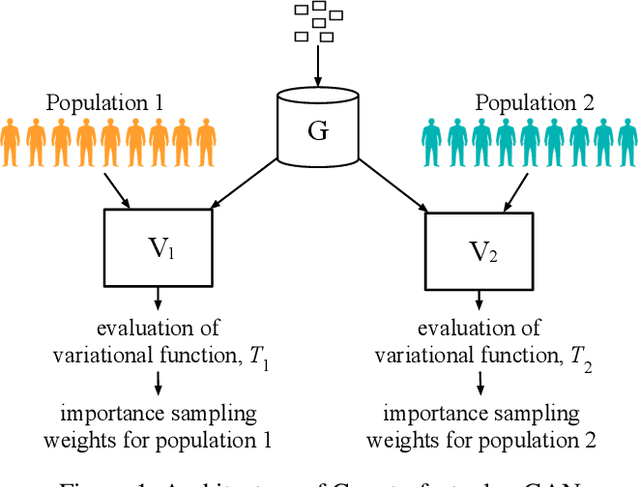
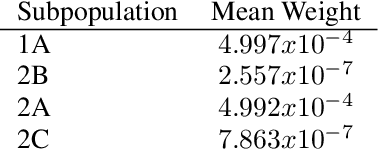
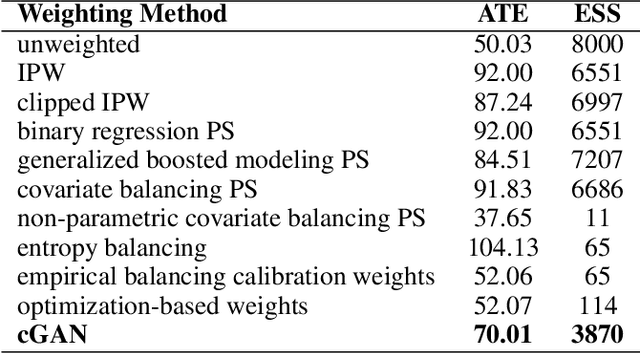
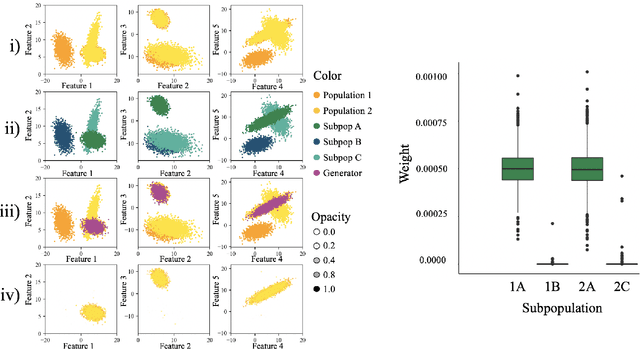
Abstract:Causal inference often relies on the counterfactual framework, which requires that treatment assignment is independent of the outcome, known as strong ignorability. Approaches to enforcing strong ignorability in causal analyses of observational data include weighting and matching methods. Effect estimates, such as the average treatment effect (ATE), are then estimated as expectations under the reweighted or matched distribution, P . The choice of P is important and can impact the interpretation of the effect estimate and the variance of effect estimates. In this work, instead of specifying P, we learn a distribution that simultaneously maximizes coverage and minimizes variance of ATE estimates. In order to learn this distribution, this research proposes a generative adversarial network (GAN)-based model called the Counterfactual $\chi$-GAN (cGAN), which also learns feature-balancing weights and supports unbiased causal estimation in the absence of unobserved confounding. Our model minimizes the Pearson $\chi^2$ divergence, which we show simultaneously maximizes coverage and minimizes the variance of importance sampling estimates. To our knowledge, this is the first such application of the Pearson $\chi^2$ divergence. We demonstrate the effectiveness of cGAN in achieving feature balance relative to established weighting methods in simulation and with real-world medical data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge