Causal Estimation with Functional Confounders
Paper and Code
Feb 17, 2021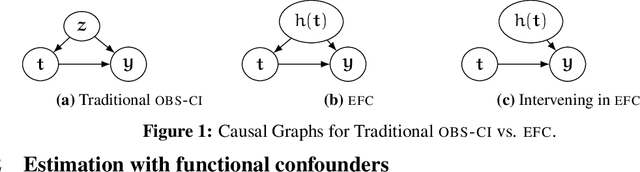

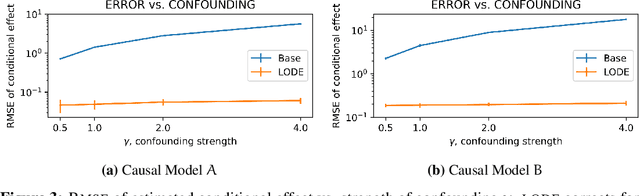
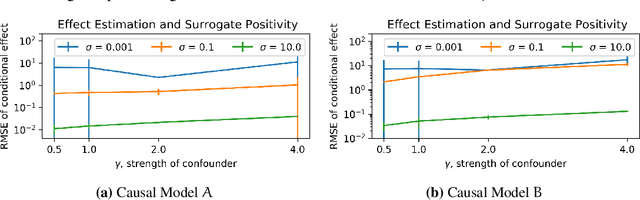
Causal inference relies on two fundamental assumptions: ignorability and positivity. We study causal inference when the true confounder value can be expressed as a function of the observed data; we call this setting estimation with functional confounders (EFC). In this setting, ignorability is satisfied, however positivity is violated, and causal inference is impossible in general. We consider two scenarios where causal effects are estimable. First, we discuss interventions on a part of the treatment called functional interventions and a sufficient condition for effect estimation of these interventions called functional positivity. Second, we develop conditions for nonparametric effect estimation based on the gradient fields of the functional confounder and the true outcome function. To estimate effects under these conditions, we develop Level-set Orthogonal Descent Estimation (LODE). Further, we prove error bounds on LODE's effect estimates, evaluate our methods on simulated and real data, and empirically demonstrate the value of EFC.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge