Adversarially-learned Inference via an Ensemble of Discrete Undirected Graphical Models

Undirected graphical models are compact representations of joint probability distributions over random variables. Given a distribution over inference tasks, graphical models of arbitrary topology can be trained using empirical risk minimization. However, when faced with new task distributions, these models (EGMs) often need to be re-trained. Instead, we propose an inference-agnostic adversarial training framework for producing an ensemble of graphical models (AGMs). The ensemble is optimized to generate data, and inference is learned as a by-product of this endeavor. AGMs perform comparably with EGMs on inference tasks that the latter were specifically optimized for. Most importantly, AGMs show significantly better generalization capabilities across distributions of inference tasks. AGMs are also on par with GibbsNet, a state-of-the-art deep neural architecture, which like AGMs, allows conditioning on any subset of random variables. Finally, AGMs allow fast data sampling, competitive with Gibbs sampling from EGMs.

Graph Element Networks: adaptive, structured computation and memory

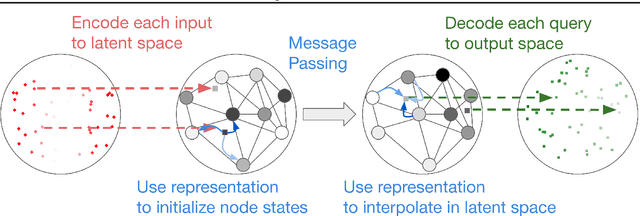
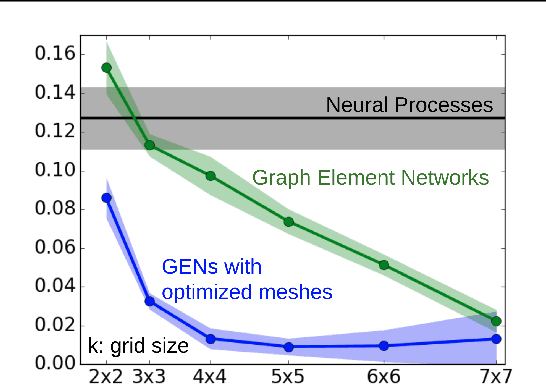
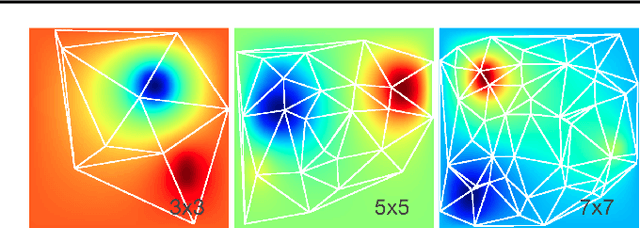
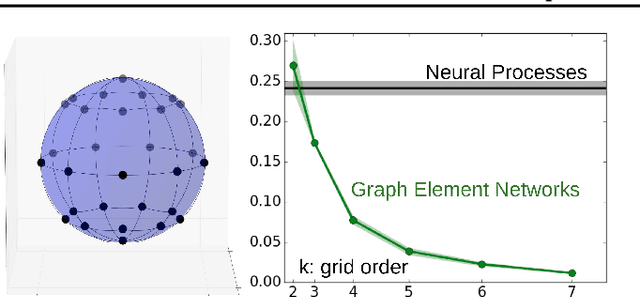
We explore the use of graph neural networks (GNNs) to model spatial processes in which there is no a priori graphical structure. Similar to finite element analysis, we assign nodes of a GNN to spatial locations and use a computational process defined on the graph to model the relationship between an initial function defined over a space and a resulting function in the same space. We use GNNs as a computational substrate, and show that the locations of the nodes in space as well as their connectivity can be optimized to focus on the most complex parts of the space. Moreover, this representational strategy allows the learned input-output relationship to generalize over the size of the underlying space and run the same model at different levels of precision, trading computation for accuracy. We demonstrate this method on a traditional PDE problem, a physical prediction problem from robotics, and learning to predict scene images from novel viewpoints.