Control Barrier Functionals: Safety-critical Control for Time Delay Systems

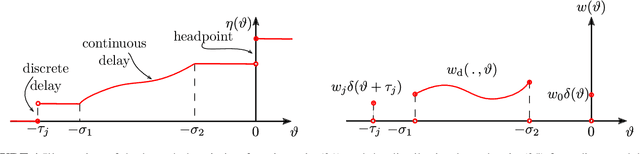
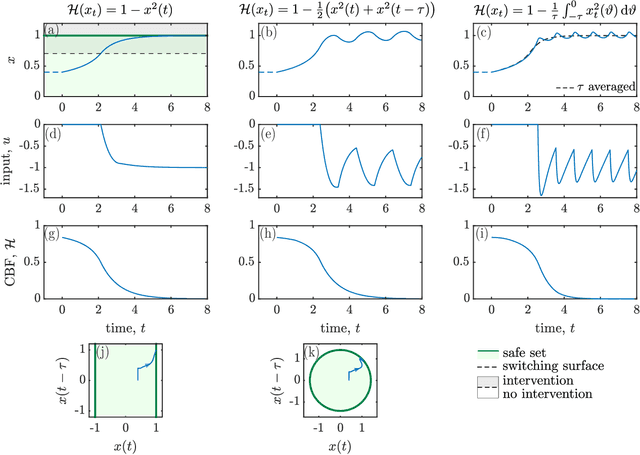
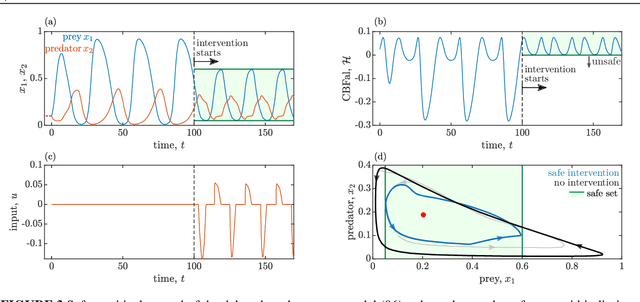
This work presents a theoretical framework for the safety-critical control of time delay systems. The theory of control barrier functions, that provides formal safety guarantees for delay-free systems, is extended to systems with state delay. The notion of control barrier functionals is introduced to attain formal safety guarantees, by enforcing the forward invariance of safe sets defined in the infinite dimensional state space. The proposed framework is able to handle multiple delays and distributed delays both in the dynamics and in the safety condition, and provides an affine constraint on the control input that yields provable safety. This constraint can be incorporated into optimization problems to synthesize pointwise optimal and provable safe controllers. The applicability of the proposed method is demonstrated by numerical simulation examples.

Input-to-State Safety with Input Delay in Longitudinal Vehicle Control

Safe longitudinal control is discussed for a connected automated truck traveling behind a preceding connected vehicle. A controller is proposed based on control barrier function theory and predictor feedback for provably safe, collision-free behavior by taking into account the significant response time of the truck as input delay and the uncertainty of its dynamical model as input disturbance. The benefits of the proposed controller compared to control designs that neglect the delay or treat the delay as disturbance are shown by numerical simulations.

Safety-Critical Control with Input Delay in Dynamic Environment

Endowing nonlinear systems with safe behavior is increasingly important in modern control. This task is particularly challenging for real-life control systems that must operate safely in dynamically changing environments. This paper develops a framework for safety-critical control in dynamic environments, by establishing the notion of environmental control barrier functions (ECBFs). The framework is able to guarantee safety even in the presence of input delay, by accounting for the evolution of the environment during the delayed response of the system. The underlying control synthesis relies on predicting the future state of the system and the environment over the delay interval, with robust safety guarantees against prediction errors. The efficacy of the proposed method is demonstrated by a simple adaptive cruise control problem and a more complex robotics application on a Segway platform.