Updating Sets of Probabilities

There are several well-known justifications for conditioning as the appropriate method for updating a single probability measure, given an observation. However, there is a significant body of work arguing for sets of probability measures, rather than single measures, as a more realistic model of uncertainty. Conditioning still makes sense in this context--we can simply condition each measure in the set individually, then combine the results--and, indeed, it seems to be the preferred updating procedure in the literature. But how justified is conditioning in this richer setting? Here we show, by considering an axiomatic account of conditioning given by van Fraassen, that the single-measure and sets-of-measures cases are very different. We show that van Fraassen's axiomatization for the former case is nowhere near sufficient for updating sets of measures. We give a considerably longer (and not as compelling) list of axioms that together force conditioning in this setting, and describe other update methods that are allowed once any of these axioms is dropped.

Logarithmic-Time Updates and Queries in Probabilistic Networks

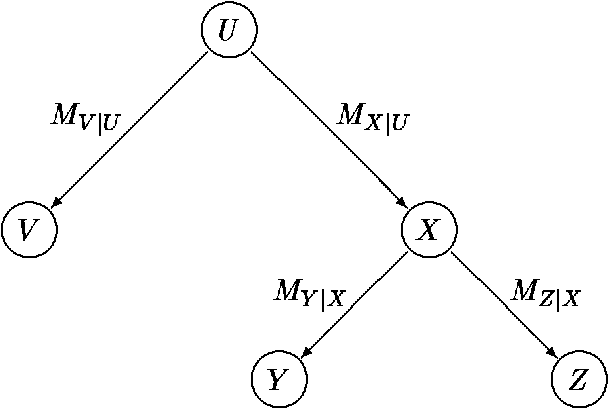
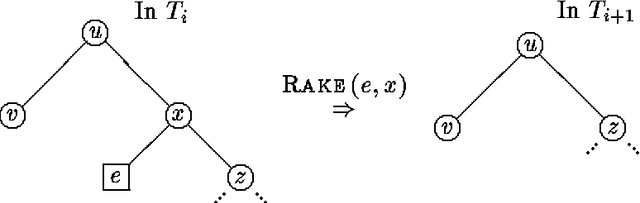
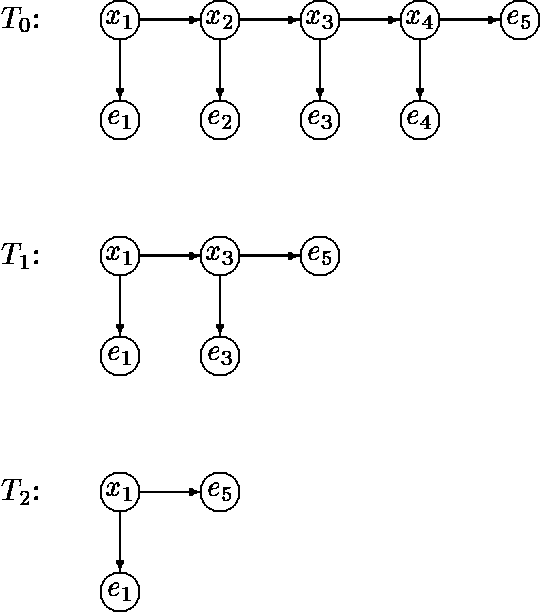
In this paper we propose a dynamic data structure that supports efficient algorithms for updating and querying singly connected Bayesian networks (causal trees and polytrees). In the conventional algorithms, new evidence in absorbed in time O(1) and queries are processed in time O(N), where N is the size of the network. We propose a practical algorithm which, after a preprocessing phase, allows us to answer queries in time O(log N) at the expense of O(logn N) time per evidence absorption. The usefulness of sub-linear processing time manifests itself in applications requiring (near) real-time response over large probabilistic databases.

Probability Estimation in Face of Irrelevant Information

In this paper, we consider one aspect of the problem of applying decision theory to the design of agents that learn how to make decisions under uncertainty. This aspect concerns how an agent can estimate probabilities for the possible states of the world, given that it only makes limited observations before committing to a decision. We show that the naive application of statistical tools can be improved upon if the agent can determine which of his observations are truly relevant to the estimation problem at hand. We give a framework in which such determinations can be made, and define an estimation procedure to use them. Our framework also suggests several extensions, which show how additional knowledge can be used to improve tile estimation procedure still further.

Generating New Beliefs From Old

In previous work [BGHK92, BGHK93], we have studied the random-worlds approach -- a particular (and quite powerful) method for generating degrees of belief (i.e., subjective probabilities) from a knowledge base consisting of objective (first-order, statistical, and default) information. But allowing a knowledge base to contain only objective information is sometimes limiting. We occasionally wish to include information about degrees of belief in the knowledge base as well, because there are contexts in which old beliefs represent important information that should influence new beliefs. In this paper, we describe three quite general techniques for extending a method that generates degrees of belief from objective information to one that can make use of degrees of belief as well. All of our techniques are bloused on well-known approaches, such as cross-entropy. We discuss general connections between the techniques and in particular show that, although conceptually and technically quite different, all of the techniques give the same answer when applied to the random-worlds method.

Graphical Models for Preference and Utility

Probabilistic independence can dramatically simplify the task of eliciting, representing, and computing with probabilities in large domains. A key technique in achieving these benefits is the idea of graphical modeling. We survey existing notions of independence for utility functions in a multi-attribute space, and suggest that these can be used to achieve similar advantages. Our new results concern conditional additive independence, which we show always has a perfect representation as separation in an undirected graph (a Markov network). Conditional additive independencies entail a particular functional for the utility function that is analogous to a product decomposition of a probability function, and confers analogous benefits. This functional form has been utilized in the Bayesian network and influence diagram literature, but generally without an explanation in terms of independence. The functional form yields a decomposition of the utility function that can greatly speed up expected utility calculations, particularly when the utility graph has a similar topology to the probabilistic network being used.

Probability Update: Conditioning vs. Cross-Entropy

Conditioning is the generally agreed-upon method for updating probability distributions when one learns that an event is certainly true. But it has been argued that we need other rules, in particular the rule of cross-entropy minimization, to handle updates that involve uncertain information. In this paper we re-examine such a case: van Fraassen's Judy Benjamin problem, which in essence asks how one might update given the value of a conditional probability. We argue that -- contrary to the suggestions in the literature -- it is possible to use simple conditionalization in this case, and thereby obtain answers that agree fully with intuition. This contrasts with proposals such as cross-entropy, which are easier to apply but can give unsatisfactory answers. Based on the lessons from this example, we speculate on some general philosophical issues concerning probability update.

Learning Bayesian Nets that Perform Well

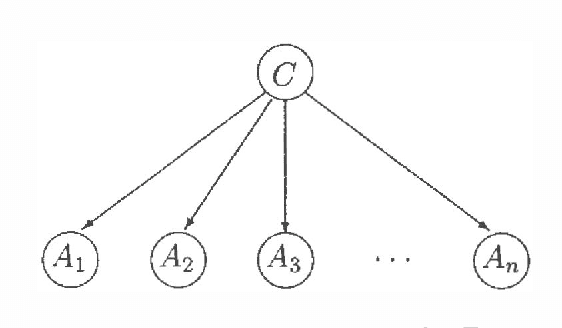
A Bayesian net (BN) is more than a succinct way to encode a probabilistic distribution; it also corresponds to a function used to answer queries. A BN can therefore be evaluated by the accuracy of the answers it returns. Many algorithms for learning BNs, however, attempt to optimize another criterion (usually likelihood, possibly augmented with a regularizing term), which is independent of the distribution of queries that are posed. This paper takes the "performance criteria" seriously, and considers the challenge of computing the BN whose performance - read "accuracy over the distribution of queries" - is optimal. We show that many aspects of this learning task are more difficult than the corresponding subtasks in the standard model.