Abinav Ravi Venkatakrishnan
Self-Supervised Out-of-Distribution Detection in Brain CT Scans
Nov 10, 2020


Abstract:Medical imaging data suffers from the limited availability of annotation because annotating 3D medical data is a time-consuming and expensive task. Moreover, even if the annotation is available, supervised learning-based approaches suffer highly imbalanced data. Most of the scans during the screening are from normal subjects, but there are also large variations in abnormal cases. To address these issues, recently, unsupervised deep anomaly detection methods that train the model on large-sized normal scans and detect abnormal scans by calculating reconstruction error have been reported. In this paper, we propose a novel self-supervised learning technique for anomaly detection. Our architecture largely consists of two parts: 1) Reconstruction and 2) predicting geometric transformations. By training the network to predict geometric transformations, the model could learn better image features and distribution of normal scans. In the test time, the geometric transformation predictor can assign the anomaly score by calculating the error between geometric transformation and prediction. Moreover, we further use self-supervised learning with context restoration for pretraining our model. By comparative experiments on clinical brain CT scans, the effectiveness of the proposed method has been verified.
Implicit Neural Solver for Time-dependent Linear PDEs with Convergence Guarantee
Oct 09, 2019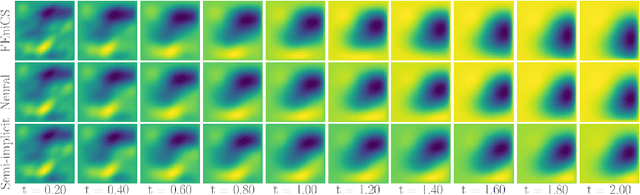

Abstract:Fast and accurate solution of time-dependent partial differential equations (PDEs) is of key interest in many research fields including physics, engineering, and biology. Generally, implicit schemes are preferred over the explicit ones for better stability and correctness. The existing implicit schemes are usually iterative and employ a general-purpose solver which may be sub-optimal for a specific class of PDEs. In this paper, we propose a neural solver to learn an optimal iterative scheme for a class of PDEs, in a data-driven fashion. We achieve this goal by modifying an iteration of an existing semi-implicit solver using a deep neural network. Further, we provide theoretical proof that our approach preserves the correctness and convergence guarantees provided by the existing iterative-solvers. We also demonstrate that our model generalizes to a different parameter setting than the one seen during training and achieves faster convergence compared to the semi-implicit schemes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge