Unimodal-Concentrated Loss: Fully Adaptive Label Distribution Learning for Ordinal Regression
Paper and Code
Apr 01, 2022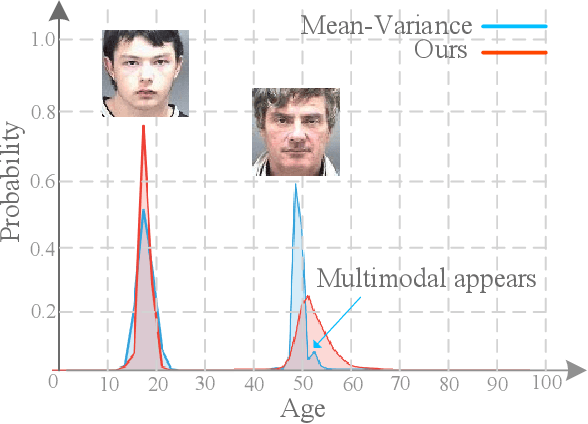
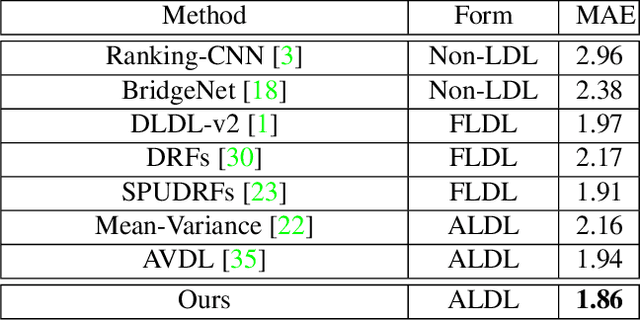
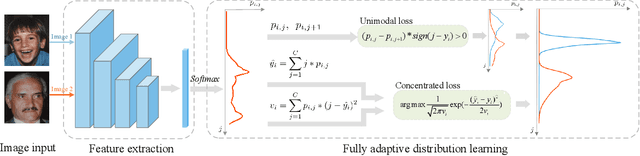
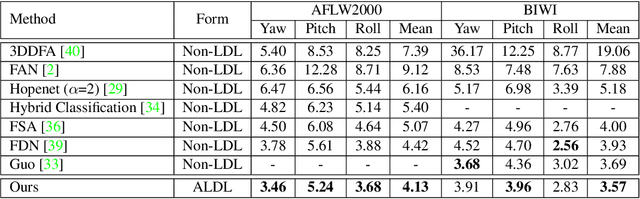
Learning from a label distribution has achieved promising results on ordinal regression tasks such as facial age and head pose estimation wherein, the concept of adaptive label distribution learning (ALDL) has drawn lots of attention recently for its superiority in theory. However, compared with the methods assuming fixed form label distribution, ALDL methods have not achieved better performance. We argue that existing ALDL algorithms do not fully exploit the intrinsic properties of ordinal regression. In this paper, we emphatically summarize that learning an adaptive label distribution on ordinal regression tasks should follow three principles. First, the probability corresponding to the ground-truth should be the highest in label distribution. Second, the probabilities of neighboring labels should decrease with the increase of distance away from the ground-truth, i.e., the distribution is unimodal. Third, the label distribution should vary with samples changing, and even be distinct for different instances with the same label, due to the different levels of difficulty and ambiguity. Under the premise of these principles, we propose a novel loss function for fully adaptive label distribution learning, namely unimodal-concentrated loss. Specifically, the unimodal loss derived from the learning to rank strategy constrains the distribution to be unimodal. Furthermore, the estimation error and the variance of the predicted distribution for a specific sample are integrated into the proposed concentrated loss to make the predicted distribution maximize at the ground-truth and vary according to the predicting uncertainty. Extensive experimental results on typical ordinal regression tasks including age and head pose estimation, show the superiority of our proposed unimodal-concentrated loss compared with existing loss functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge