Towards Practical Lottery Ticket Hypothesis for Adversarial Training
Paper and Code
Mar 06, 2020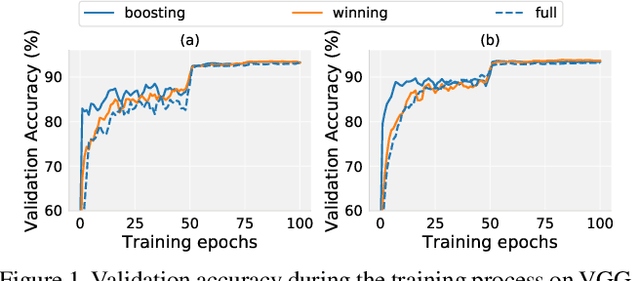

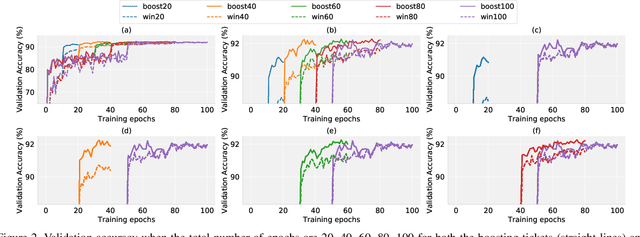

Recent research has proposed the lottery ticket hypothesis, suggesting that for a deep neural network, there exist trainable sub-networks performing equally or better than the original model with commensurate training steps. While this discovery is insightful, finding proper sub-networks requires iterative training and pruning. The high cost incurred limits the applications of the lottery ticket hypothesis. We show there exists a subset of the aforementioned sub-networks that converge significantly faster during the training process and thus can mitigate the cost issue. We conduct extensive experiments to show such sub-networks consistently exist across various model structures for a restrictive setting of hyperparameters ($e.g.$, carefully selected learning rate, pruning ratio, and model capacity). As a practical application of our findings, we demonstrate that such sub-networks can help in cutting down the total time of adversarial training, a standard approach to improve robustness, by up to 49\% on CIFAR-10 to achieve the state-of-the-art robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge