Towards Dynamic Graph Neural Networks with Provably High-Order Expressive Power
Paper and Code
Oct 02, 2024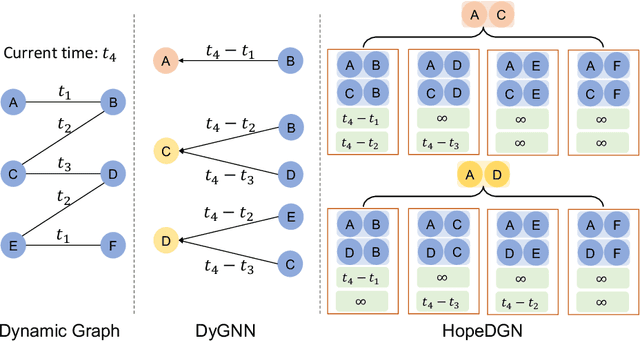
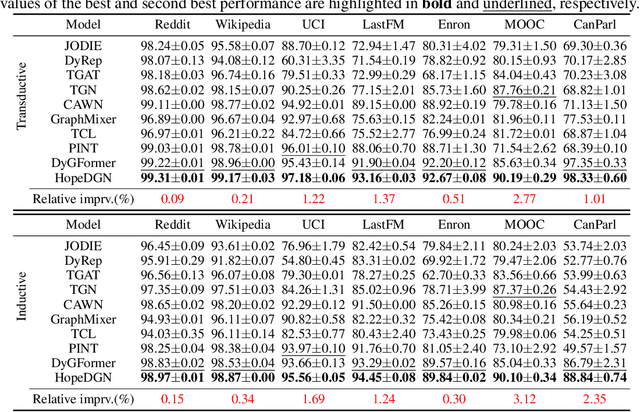
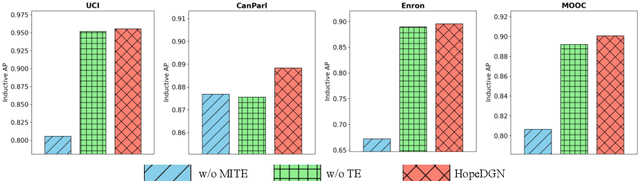
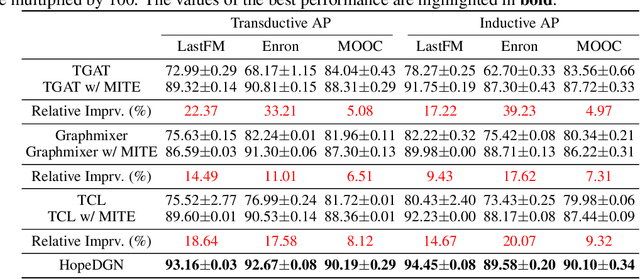
Dynamic Graph Neural Networks (DyGNNs) have garnered increasing research attention for learning representations on evolving graphs. Despite their effectiveness, the limited expressive power of existing DyGNNs hinders them from capturing important evolving patterns of dynamic graphs. Although some works attempt to enhance expressive capability with heuristic features, there remains a lack of DyGNN frameworks with provable and quantifiable high-order expressive power. To address this research gap, we firstly propose the k-dimensional Dynamic WL tests (k-DWL) as the referencing algorithms to quantify the expressive power of DyGNNs. We demonstrate that the expressive power of existing DyGNNs is upper bounded by the 1-DWL test. To enhance the expressive power, we propose Dynamic Graph Neural Network with High-order expressive power (HopeDGN), which updates the representation of central node pair by aggregating the interaction history with neighboring node pairs. Our theoretical results demonstrate that HopeDGN can achieve expressive power equivalent to the 2-DWL test. We then present a Transformer-based implementation for the local variant of HopeDGN. Experimental results show that HopeDGN achieved performance improvements of up to 3.12%, demonstrating the effectiveness of HopeDGN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge