The Mutex Watershed and its Objective: Efficient, Parameter-Free Image Partitioning

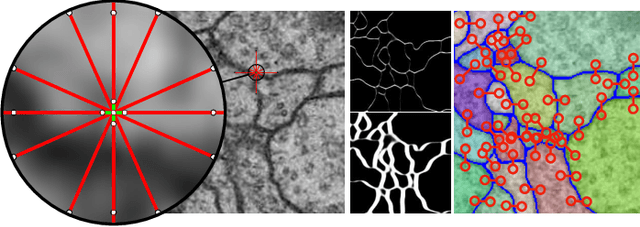
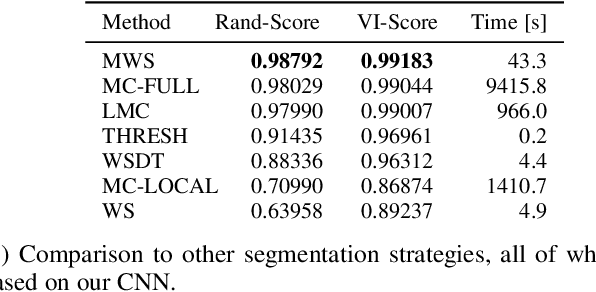
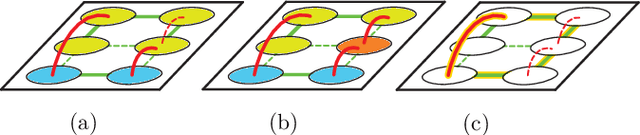
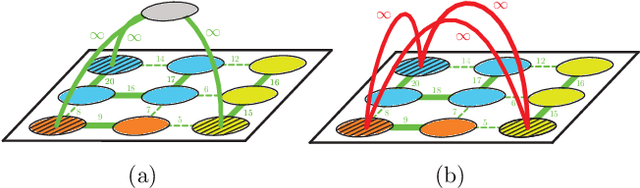
Image partitioning, or segmentation without semantics, is the task of decomposing an image into distinct segments, or equivalently to detect closed contours. Most prior work either requires seeds, one per segment; or a threshold; or formulates the task as multicut / correlation clustering, an NP-hard problem. Here, we propose a greedy algorithm for signed graph partitioning, the "Mutex Watershed". Unlike seeded watershed, the algorithm can accommodate not only attractive but also repulsive cues, allowing it to find a previously unspecified number of segments without the need for explicit seeds or a tunable threshold. We also prove that this simple algorithm solves to global optimality an objective function that is intimately related to the multicut / correlation clustering integer linear programming formulation. The algorithm is deterministic, very simple to implement, and has empirically linearithmic complexity. When presented with short-range attractive and long-range repulsive cues from a deep neural network, the Mutex Watershed gives the best results currently known for the competitive ISBI 2012 EM segmentation benchmark.