Seeking Patterns, Not just Memorizing Procedures: Contrastive Learning for Solving Math Word Problems
Paper and Code
Oct 16, 2021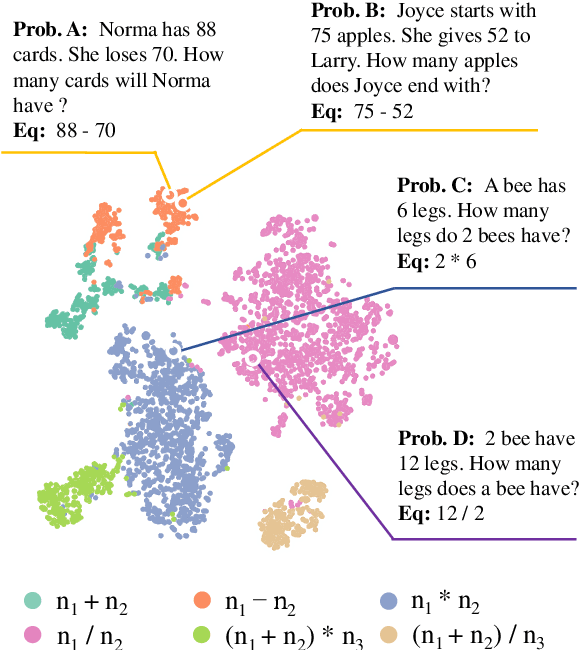

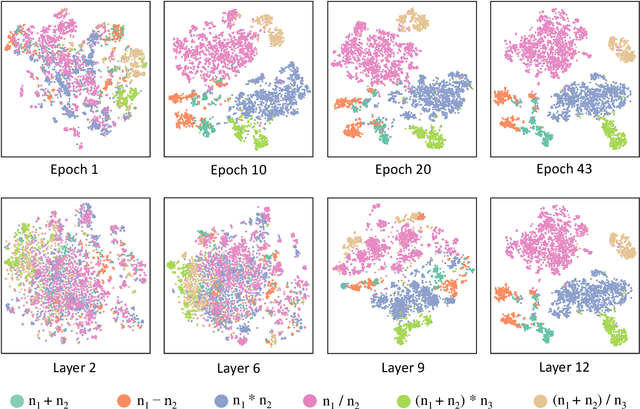
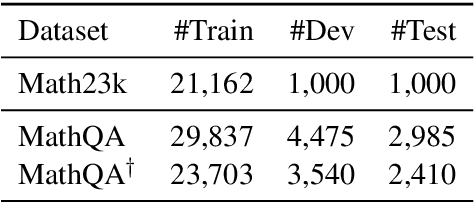
Math Word Problem (MWP) solving needs to discover the quantitative relationships over natural language narratives. Recent work shows that existing models memorize procedures from context and rely on shallow heuristics to solve MWPs. In this paper, we look at this issue and argue that the cause is a lack of overall understanding of MWP patterns. We first investigate how a neural network understands patterns only from semantics, and observe that, if the prototype equations are the same, most problems get closer representations and those representations apart from them or close to other prototypes tend to produce wrong solutions. Inspired by it, we propose a contrastive learning approach, where the neural network perceives the divergence of patterns. We collect contrastive examples by converting the prototype equation into a tree and seeking similar tree structures. The solving model is trained with an auxiliary objective on the collected examples, resulting in the representations of problems with similar prototypes being pulled closer. We conduct experiments on the Chinese dataset Math23k and the English dataset MathQA. Our method greatly improves the performance in monolingual and multilingual settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge