Scalable Inference for Nonparametric Hawkes Process Using Pólya-Gamma Augmentation
Paper and Code
Oct 29, 2019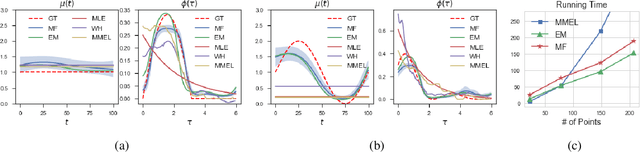
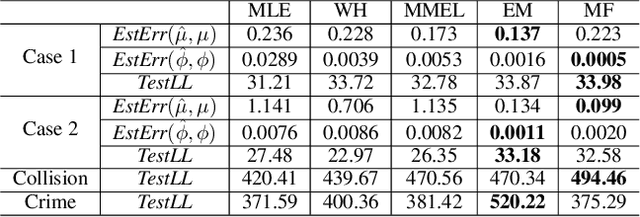

In this paper, we consider the sigmoid Gaussian Hawkes process model: the baseline intensity and triggering kernel of Hawkes process are both modeled as the sigmoid transformation of random trajectories drawn from Gaussian processes (GP). By introducing auxiliary latent random variables (branching structure, P\'{o}lya-Gamma random variables and latent marked Poisson processes), the likelihood is converted to two decoupled components with a Gaussian form which allows for an efficient conjugate analytical inference. Using the augmented likelihood, we derive an expectation-maximization (EM) algorithm to obtain the maximum a posteriori (MAP) estimate. Furthermore, we extend the EM algorithm to an efficient approximate Bayesian inference algorithm: mean-field variational inference. We demonstrate the performance of two algorithms on simulated fictitious data. Experiments on real data show that our proposed inference algorithms can recover well the underlying prompting characteristics efficiently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge