Reinforcement Learning in Presence of Discrete Markovian Context Evolution
Paper and Code
Feb 14, 2022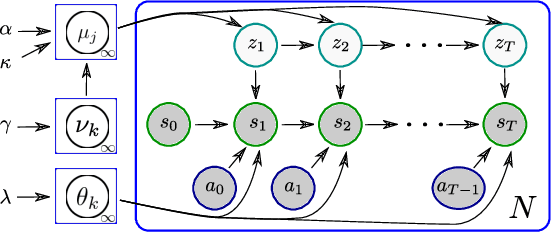
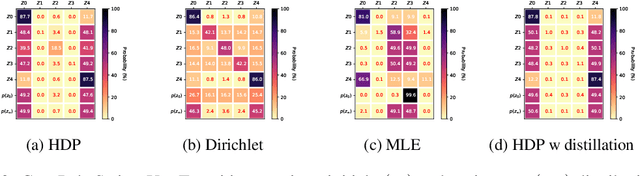
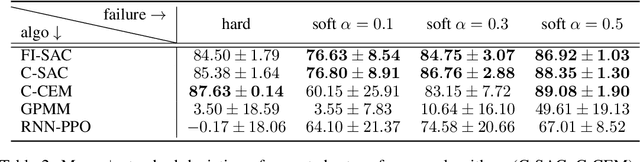
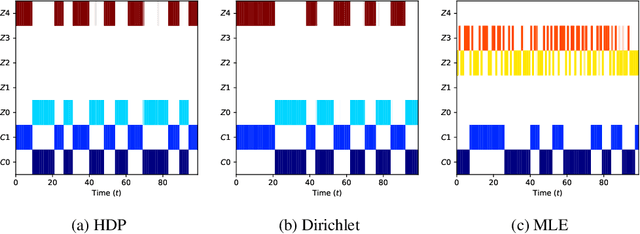
We consider a context-dependent Reinforcement Learning (RL) setting, which is characterized by: a) an unknown finite number of not directly observable contexts; b) abrupt (discontinuous) context changes occurring during an episode; and c) Markovian context evolution. We argue that this challenging case is often met in applications and we tackle it using a Bayesian approach and variational inference. We adapt a sticky Hierarchical Dirichlet Process (HDP) prior for model learning, which is arguably best-suited for Markov process modeling. We then derive a context distillation procedure, which identifies and removes spurious contexts in an unsupervised fashion. We argue that the combination of these two components allows to infer the number of contexts from data thus dealing with the context cardinality assumption. We then find the representation of the optimal policy enabling efficient policy learning using off-the-shelf RL algorithms. Finally, we demonstrate empirically (using gym environments cart-pole swing-up, drone, intersection) that our approach succeeds where state-of-the-art methods of other frameworks fail and elaborate on the reasons for such failures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge