Precision Learning: Reconstruction Filter Kernel Discretization
Paper and Code
Jul 09, 2018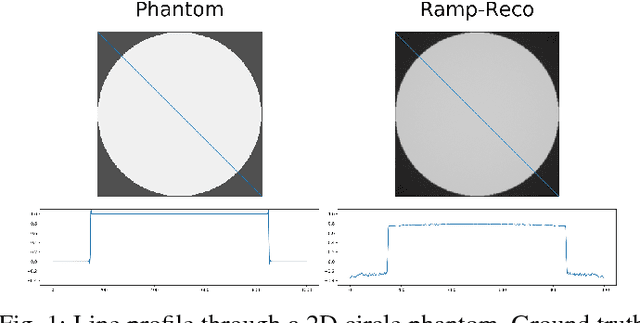
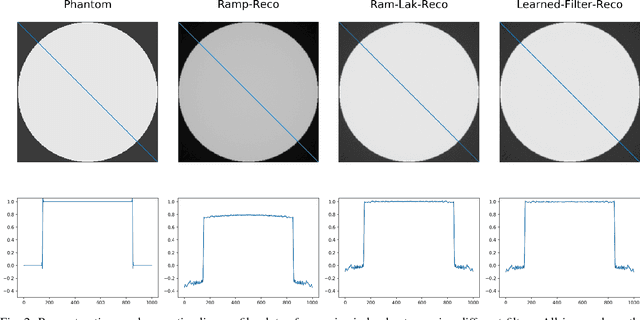
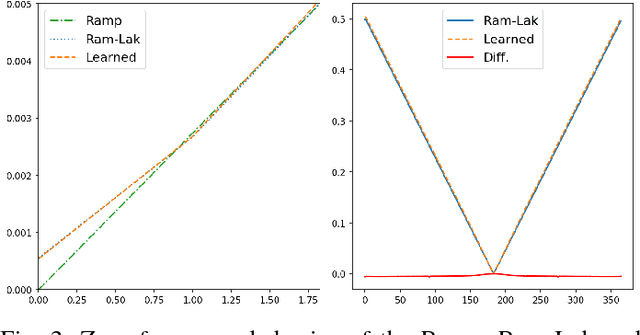
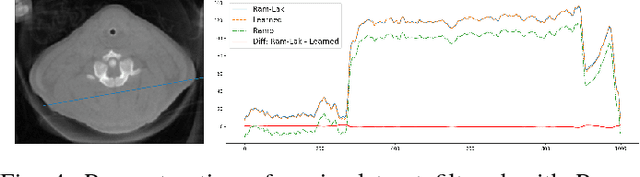
In this paper, we present substantial evidence that a deep neural network will intrinsically learn the appropriate way to discretize the ideal continuous reconstruction filter. Currently, the Ram-Lak filter or heuristic filters which impose different noise assumptions are used for filtered back-projection. All of these, however, inhibit a fully data-driven reconstruction deep learning approach. In addition, the heuristic filters are not chosen in an optimal sense. To tackle this issue, we propose a formulation to directly learn the reconstruction filter. The filter is initialized with the ideal Ramp filter as a strong pre-training and learned in frequency domain. We compare the learned filter with the Ram-Lak and the Ramp filter on a numerical phantom as well as on a real CT dataset. The results show that the network properly discretizes the continuous Ramp filter and converges towards the Ram-Lak solution. In our view these observations are interesting to gain a better understanding of deep learning techniques and traditional analytic techniques such as Wiener filtering and discretization theory. Furthermore, this will allow fully trainable data-driven reconstruction deep learning approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge